Capítulo 11 Imputación múltiple en encuestas de hogares
La no respuesta en encuestas de hogares es un fenómenos que desde siempre ha sucedido, más ahora después de la pandemia del Covid -19. Esto sucede por muchas razones, por ejemplo, la longitud de los cuestionarios en las encuestas, el no conocer algunas características particulares del hogar, la renuencia por entregar información sensible, entre otras. Si la no respuesta en algún indicador del estudio es muy alto, puede poner en riesgo la calidad de las estimaciones que se obtienen utilizando los estimadores clásicos.
Debido a este problema, se ha avanzado en la literatura especializada metodologías que permiten atacar este problema, el cual es una realidad en todas las encuestas de hogares en los distintos países. 427
En este sentido, alguno de los avances en la teoría de los métodos en el contexto de muestras comlejas son: imputación múltiple (MI; Van Buuren, 2012; Carpenter y Kenward, 2013; Berglund y Heeringa, 2014; Stata Corp, 2015; Raghunathan, 2016). También se encuentra en la literatura métodos como el de imputación fraccional (FI; Kim y Fuller, 2004; Kim y Shao, 2014), el Bootstrap Bayesiano de Población Finita (Zhou et al., 2016a,b), y métodos de máxima verosimilitud como los de Chambers et al., (2012).
El objetivo principal de este capítulo es abordar el problema de la falta de datos en encuestas de hogares, revisar las posibles causas, el impacto que tiene en la estimación de los indicadores, y mostrar algunas soluciones a la falta de datos en las encuesta.
Siguiendo las ideas anteriores, sea \(\boldsymbol{X}_{n \times p} = x_{ij}\) una matriz completa (sin valores perdidos) de tal forma que \(X_{ij}\) es el valor de la variable \(j\) con \(j=1, \dots, p\) e \(i\) con \(i=1, \dots, n\). Adicionalmente, se define \(\boldsymbol{M}_{n \times p} = m_{ij}\) una matriz indicadoradonde \(m_{ij} = 1\) si el valor de \(x_{ij}\) es un dato perdido y \(m_{ij}=0\) si \(x_{ij}\) está presente.
Ahora bie, note que la matriz \(M\) describe el patrón de missing (datos faltantes), y su media marginal de columna puede ser interpretada como la probabilidad de que \(x_{ij}\) sea missing. A continuación, se describen alguna de las particularidades de la matriz \(\boldsymbol{M}_{n \times p}\):
La matriz \(\boldsymbol{M}_{n \times p}\) presenta un comportamiento completamente al azar (MCAR): si la probabilidad de respuesta es independiente de las variables observadas y de las no observadas completamente. El mecanismo de pérdida es ignorable tanto para inferencias basadas en muestreo como en máxima verosimilitud.
Los valores de la matriz \(\boldsymbol{M}_{n \times p}\) son al azar (MAR): si la probabilidad de respuesta es independiente de las variables no observadas completamente y no de las observadas. El mecanismo de pérdida es ignorable para inferencias basadas en máxima verosimilitud.
Los datos no están perdidos al azar (MNAR): si la probabilidad de respuesta no es independiente de las variables no observadas completamente y posiblemente, también, de las observadas. El mecanismo de pérdida es no ignorable.
En las dos figuras siguientes, se ilustran los casos de observaciones perdidas de manera aleatoria y con un patrón identificado:
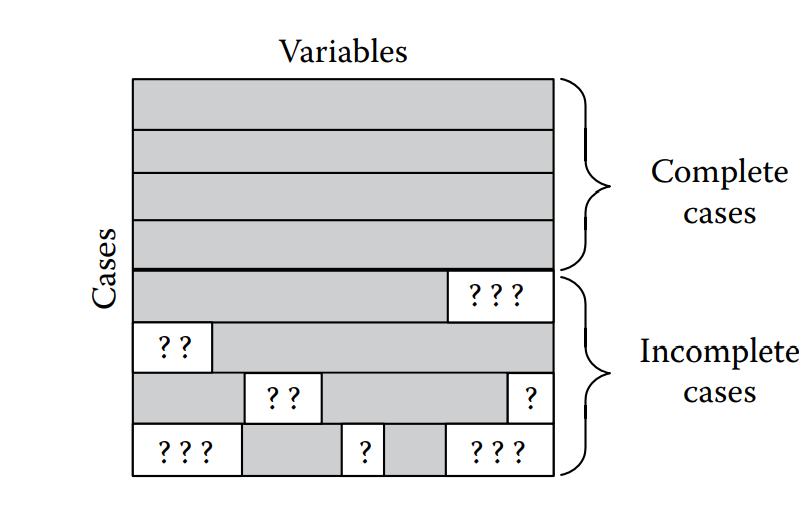
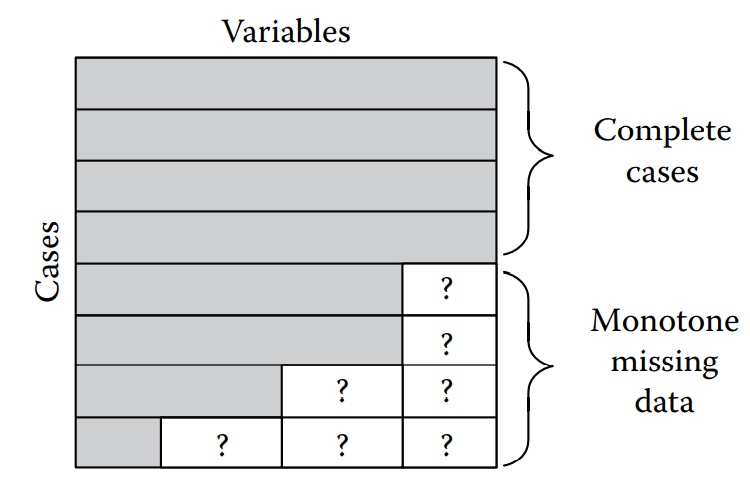
Como se ha venido trabajando en los capítulos anteriores, primero carguemos la base de datos con la muestra seleccionada y con el fin de poder ejemplificar el tratamiento de datos faltantes, se incluiran manualmente “valores perdidos”. En este sentido, la lectura de la base se hará a continuación:
encuesta <- readRDS("Data/encuesta.rds") Se filtran encuestados mayores a 15 años y se calcula la proporción de la población desempleada, inactiva y empleada antes de generar los valores faltantes. Pero antes de eso, se cargan todas las librerías que se utilizarán en este capítulo:
knitr::opts_chunk$set(cache = FALSE, warning = FALSE, message = FALSE, error = FALSE)
#options(digits = 4)
options(tinytex.verbose = TRUE)
library (survey)
library(srvyr)
library(convey)
library(TeachingSampling)
library(printr)
library(stargazer)
library(broom)
library(jtools)
library(modelsummary)
library(patchwork)
library(ggplot2)Cálculo de las proprociones de personas desempleadas, inactivas y empleados:
encuesta<- encuesta |> filter(Age >= 15)
(tab_antes <- prop.table(table(encuesta$Employment)))| Unemployed | Inactive | Employed |
|---|---|---|
| 0.0409792 | 0.373603 | 0.5854178 |
También se calcula el promedio de ingresos en al muestra:
(med_antes <- mean(encuesta$Income, na.rm = TRUE))## [1] 604.2494Luego de los conteos anteriores, se genera un 20% de valores faltantes siguiendo un esquema MCAR como sigue:
set.seed(1234)
encuesta_MCAR <- sample_frac(encuesta, 0.8 )
dat_plot <- bind_rows(
list(encuesta_MCAR = encuesta_MCAR,
encuesta = encuesta), .id = "Caso" )Ahora bien, para poder ver el efecto de la inclusión de datos faltantes de manera gráfica por zona y sexo para la variable ingreso, se realizan las siguientes gráficas:
p1 <- ggplot(dat_plot, aes(x=Zone, y = Income)) +
geom_boxplot() + facet_grid(.~Caso) + theme_bw()+
geom_hline(yintercept = mean(encuesta$Income),
col = "red")
p2 <- ggplot(dat_plot, aes(x=Sex, y = Income)) +
geom_boxplot() + facet_grid(.~Caso) +theme_bw()+
geom_hline(yintercept = mean(encuesta$Income),
col = "red")
library(patchwork)
p1|p2Como se puede observar en las gráficas anteriores, la distribución de los ingresos por Zona y Sexo se mantiene similar con o sin presencia de la no respuesta. Esto se debe a que la no respuesta que se incluyó no depende de la variable de estudio.
Ahora bien, analizando la variable de interés se tiene que tampoco hay cambios distribucionales notables entre las distribuciones con y sin datos faltantes por sexo, como se puede observar a continuación:
p1 <- ggplot(dat_plot, aes(x = Income, fill = Caso)) +
geom_density(alpha = 0.3) + theme_bw() +
theme(legend.position = "bottom") +
geom_vline(xintercept = mean(encuesta$Income),
col = "red")
p2 <- ggplot(dat_plot, aes(x = Income, fill = Caso)) +
geom_density(alpha = 0.3) + facet_grid(.~Sex) +
theme_bw()+
geom_vline(xintercept = mean(encuesta$Income),
col = "red") +
theme(legend.position = "none")
(p1/p2)Si graficamos ahora la varibale gastos, se tienen los mismos resultados que para ingresos.
p1 <- ggplot(dat_plot, aes(x = Expenditure, fill = Caso)) +
geom_density(alpha = 0.3) + theme_bw() +
theme(legend.position = "bottom") +
geom_vline(xintercept = mean(encuesta$Expenditure),
col = "red")
p2 <- ggplot(dat_plot, aes(x = Expenditure, fill = Caso)) +
geom_density(alpha = 0.3) + facet_grid(.~Sex) +
theme_bw()+
geom_vline(xintercept = mean(encuesta$Expenditure),
col = "red") +
theme(legend.position = "none")
(p1/p2)Por otro lado, simulemos ahora una pérdida de información MAR como sigue:
library(TeachingSampling)
set.seed(1234)
temp_estrato <- paste0(encuesta$Zone, encuesta$Sex)
table(temp_estrato)| RuralFemale | RuralMale | UrbanFemale | UrbanMale |
|---|---|---|---|
| 481 | 428 | 531 | 439 |
sel <- S.STSI(S = temp_estrato,
Nh = c(481,428,531,439),
nh = c(20, 380, 20,280))
encuesta_MAR <- encuesta[-sel,]
dat_plot2 <- bind_rows(
list(encuesta_MAR = encuesta_MAR,
encuesta = encuesta), .id = "Caso" )El código anterior utiliza la librería TeachingSampling para realizar un muestreo aleatorio estratificado. Primero, se establece la semilla aleatoria en 1234 para asegurarse de que los resultados sean reproducibles. A continuación, se crea una variable llamada temp_estrato que combina dos variables de la encuesta “Zone” y “Sex” utilizando la función “paste0” para crear grupos de estratos. La función table se usa para mostrar la frecuencia de cada estrato.
Luego, se realiza el muestreo estratificado utilizando la función S.STSI que toma los siguientes argumentos:
- “S”: el vector de estratos creado anteriormente
- “Nh”: el número de unidades en cada estrato (en este caso, 469, 411, 510 y 390)
- “nh”: el tamaño de muestra deseado para cada estrato (en este caso, 20, 380, 20 y 280)
El resultado del muestreo estratificado es un vector de índices de fila que corresponden a las observaciones seleccionadas para la muestra. Luego, se crea un nuevo conjunto de datos llamado “encuesta_MAR” que excluye las observaciones seleccionadas en la muestra.
Finalmente, se usa la función bind_rows del paquete dplyr para unir los dos conjuntos de datos, “encuesta” y “encuesta_MAR”, en un solo conjunto de datos llamado “dat_plot2”, con una nueva variable “Caso” que indica el caso de cada observación en el conjunto de datos.
Observemos gráficamente el efecto de la perdida de dinformación en una encuesta en un esquema MAR:
p1 <- ggplot(dat_plot2, aes(x= Caso, y = Expenditure)) +
geom_hline(yintercept = mean(encuesta$Expenditure),
col = "red") +
geom_boxplot() +
facet_grid(Zone~Sex) + theme_bw()
p1En el gráfico anterior se logra observar un cambio en la distribución de los datos en las distintas desagregaciones cuando en la encuesta no se tiene pérdida de información y cuando sí se tiene con un esquema MAR. Naturalmente, esto afectaría en las estimaciones finales que se hagan de los parámetros estudiados.
Con mayor claridad, se puede ver el cambio distribucional en la siguiente gráfica:
p1 <- ggplot(dat_plot2, aes(x = Income, fill = Caso)) +
geom_density(alpha = 0.3) + theme_bw() +
theme(legend.position = "bottom") +
geom_vline(xintercept = mean(encuesta$Income),
col = "red")
p2 <- ggplot(dat_plot2, aes(x = Income, fill = Caso)) +
facet_grid(.~Sex) +
geom_density(alpha = 0.3) + theme_bw() +
theme(legend.position = "none") +
geom_vline(xintercept = mean(encuesta$Income),
col = "red")
p1/p2Este comportamiento es natural que suceda en un esquema MAR de datos faltantes puesto que, como se mencionó anteriormente, cuando se dice que los datos faltantes están “missing at random” (MAR), significa que la probabilidad de que los datos estén ausentes está relacionada con los valores observados en otras variables del conjunto de datos. En otras palabras, la probabilidad de que un valor esté ausente no está relacionada con el valor real del dato en sí mismo, sino que depende de la distribución de los datos en otras variables.
La ventaja que tienen los mecanismo de missing MAR es que se puede estimar el valor real de los datos faltantes utilizando la información de otras variables disponibles en el conjunto de datos. Esto puede mejorar la calidad de los resultados de los análisis y evitar la necesidad de descartar observaciones con datos faltantes.
Otra gráfica en donde se evidencia el cambio de distribución de los gastos entre hombres y mujeres.
p1 <- ggplot(dat_plot2,
aes(x = Expenditure, fill = Caso)) +
geom_density(alpha = 0.3) + theme_bw() +
theme(legend.position = "bottom") +
geom_vline(
xintercept = mean(encuesta$Expenditure),
col = "red")
p2 <- ggplot(dat_plot2,
aes(x = Expenditure, fill = Caso)) +
facet_grid(.~Sex) +
geom_density(alpha = 0.3) + theme_bw() +
theme(legend.position = "none") +
geom_vline(
xintercept = mean(encuesta$Expenditure),
col = "red")
p1/p2Ahora bien, para seguir con la ejemplificación de los esquemas de datos faltantes, generemos ahora un esquema de pérdida de información en una encuesta NMAR (siglas en inglés de “Not Missing at Random”). Como se mencionó al inicio de este capítulo, en este tipo de esquema, la probabilidad de que un dato falte está relacionada con el propio valor de ese dato, es decir, la probabilidad de que falte un dato no es aleatoria y depende de alguna característica o variable del propio dato.
En otras palabras, en un esquema aleatorio NMAR, la probabilidad de que falte un dato no es independiente del valor de ese dato, sino que está influenciada por algún factor que puede estar relacionado con el fenómeno que se está estudiando. Esto puede llevar a que los datos faltantes introduzcan un sesgo en los resultados del análisis estadístico, lo que hace que el manejo adecuado de los datos faltantes en este tipo de esquemas sea particularmente importante en la investigación.
encuesta_MNAR <- encuesta %>%
arrange((Income)) %>%
slice(1:1300L)
dat_plot3 <- bind_rows(
list(encuesta_MNAR = encuesta_MNAR,
encuesta = encuesta), .id = "Caso" )El código anterior tiene como objetivo crear un nuevo conjunto de datos llamado encuesta_MNAR que contiene las primeras 1300 observaciones del conjunto de datos original encuesta, ordenadas por la variable Income. Luego, el código une el conjunto de datos original encuesta con el conjunto de datos encuesta_MNAR usando la función bind_rows(), y crea una nueva variable llamada “Caso” que indica la fuente de los datos.
Ahora bien, para ver el efecto que tiene en una encuesta el tener datos faltante con esquema NMAR, se ilustran los siguientes gráficos:
p1 <- ggplot(dat_plot3, aes(x = Income, fill = Caso)) +
geom_density(alpha = 0.2) + theme_bw() +
theme(legend.position = "bottom") +
geom_vline(
xintercept = mean(encuesta$Income),
col = "red") +
geom_vline(
xintercept = mean(encuesta_MNAR$Income),
col = "blue")
p1Como se puede observar en la gráfica anterior, la distribución de los ingresos cambia notablemente cuando se tienen datos faltantes con esquema NMAR, lo mismo sucede con la variable gastos, como se puede observar en la siguiente gráfica:
p1 <- ggplot(dat_plot3,
aes(x = Expenditure, fill = Caso)) +
geom_density(alpha = 0.2) + theme_bw() +
theme(legend.position = "bottom") +
geom_vline(
xintercept = mean(encuesta$Expenditure),
col = "red") +
geom_vline(
xintercept = mean(encuesta_MNAR$Expenditure),
col = "blue")
p1Para ver más al detalle el impacto que tiene la no respuesta con un esquema NMAR, a continuación se muestra una gráfica del ingreso discriminada por sexo y por zona. También se nota un cambio en la distribución de los ingresos significativos.
p1 <- ggplot(dat_plot3, aes(x= Caso, y = Income)) +
geom_hline(yintercept = mean(encuesta$Income),
col = "red") + geom_boxplot() +
facet_grid(Zone~Sex) + theme_bw()
p1Para efectos de ejemplificar la solución del problema a los datos faltantes en una encuesta de hogares, generemos la siguiente base de datos:
encuesta <- full_join(
encuesta,
encuesta_MCAR %>%
dplyr::select(HHID, PersonID, Income, Employment) %>%
mutate(
Income_missin = Income,
Employment_missin = Employment,
Employment = NULL,
Income = NULL
)
)El código anterior utiliza la función full_join() de la librería dplyr de ´R´ para combinar dos conjuntos de datos: encuesta y encuesta_MCAR. La combinación se realiza mediante la unión completa (o full join), que devuelve todas las filas de ambas tablas, uniendo las filas con valores coincidentes y rellenando con valores faltantes para las columnas que no tienen una coincidencia en ambas tablas.
La segunda Base de datos, encuesta_MCAR, se transforma previamente con las siguientes operaciones:
Se seleccionan las columnas HHID, PersonID, Income y Employment mediante la función dplyr::select().
Se agregan dos nuevas columnas, Income_missin y Employment_missin, utilizando la función mutate().
Los valores de estas columnas son idénticos a los de las columnas Income y Employment, respectivamente. Las columnas Income y Employment se eliminan del conjunto de datos utilizando la función mutate() y asignando el valor NULL a ambas columnas. Finalmente, el resultado de la unión completa se asigna a la variable encuesta.
Ahora bien, para tener como referencia el porcentaje de datos faltantes, se ejecuta el siguiente comando:
encuesta %>% group_by(Zone) %>%
summarise(Income = sum(is.na(Income_missin) / n()))| Zone | Income |
|---|---|
| Rural | 0.2079208 |
| Urban | 0.1927835 |
encuesta %>% group_by(Sex) %>%
summarise(Income = sum(is.na(Income_missin) / n()))| Sex | Income |
|---|---|
| Female | 0.1837945 |
| Male | 0.2191465 |