5.4 Modelos multiparamétricos
- La distribución normal univariada que tiene dos parámetros: la media \(\theta\) y la varianza \(\sigma^2\).
- La distribución multinomial cuyo parámetro es un vector de probabilidades \(\boldsymbol{\theta}\).
5.4.1 Modelo de unidad: Normal con media y varianza desconocida
Supongamos que se dispone de realizaciones de un conjunto de variables independientes e idénticamente distribuidas \(Y_1,\cdots,Y_n\sim N(\theta,\sigma^2)\). Cuando se desconoce tanto la media como la varianza de la distribución es necesario plantear diversos enfoques y situarse en el más conveniente, según el contexto del problema. En términos de la asignación de las distribuciones previas para \(\theta\) y \(\sigma^2\) es posible:
- Suponer que la distribución previa \(p(\theta)\) es independiente de la distribución previa \(p(\sigma^2)\) y que ambas distribuciones son informativas.
- Suponer que la distribución previa \(p(\theta)\) es independiente de la distribución previa \(p(\sigma^2)\) y que ambas distribuciones son no informativas.
- Suponer que la distribución previa para \(\theta\) depende de \(\sigma^2\) y escribirla como \(p(\theta \mid \sigma^2)\), mientras que la distribución previa de \(\sigma^2\) no depende de \(\theta\) y se puede escribir como \(p(\sigma^2)\).
La distribución previa para el parámetro \(\theta\) será
\[ \begin{equation*} \theta \sim Normal(0,10000) \end{equation*} \]
Y la distribución previa para el parámetro \(\sigma^2\) será
\[ \begin{equation*} \sigma^2 \sim IG(0.0001,0.0001) \end{equation*} \]
La distribución posterior condicional de \(\theta\) es
\[ \begin{equation} \theta \mid \sigma^2,\mathbf{Y} \sim Normal(\mu_n,\tau_n^2) \end{equation} \]
En donde las expresiones para \(\mu_n\) y \(\tau_n^2\) están dados previamente.
En el siguiente enlace enconará el libro: Modelos Bayesianos con R y STAN donde puede profundizar en el desarrollo matemático de los resultados anteriores.
Obejtivo
Estimar el ingreso medio de las personas, es decir,
\[ \bar{Y} = \frac{\sum_Uy_i}{N} \] donde, \(y_i\) es el ingreso de las personas. El estimador de \(\bar{Y}\) esta dado por \[ \hat{\bar{Y}} = \frac{\sum_{s}w_{i}y_{i}}{\sum_s{w_i}} \] y obtener \(\widehat{Var}\left(\hat{\bar{Y}}\right)\).
5.4.1.1 Práctica en STAN
Sea \(Y\) el logaritmo del ingreso
dataNormal <- encuesta %>%
transmute(dam_ee,
logIngreso = log(ingcorte +1)) %>%
filter(dam_ee == 1)Creando código de STAN
data {
int<lower=0> n;
real y[n];
}
parameters {
real sigma;
real theta;
}
transformed parameters {
real sigma2;
sigma2 = pow(sigma, 2);
}
model {
y ~ normal(theta, sigma);
theta ~ normal(0, 1000);
sigma2 ~ inv_gamma(0.001, 0.001);
}
generated quantities {
real ypred[n]; // vector de longitud n
for(kk in 1:n){
ypred[kk] = normal_rng(theta,sigma);
}
}Preparando el código de STAN
NormalMeanVar <- "Recursos/Día2/Sesion1/Data/modelosStan/5NormalMeanVar.stan" Organizando datos para STAN
sample_data <- list(n = nrow(dataNormal),
y = dataNormal$logIngreso)Para ejecutar STAN en R tenemos la librería rstan
options(mc.cores = parallel::detectCores())
model_NormalMedia <- stan(
file = NormalMeanVar,
data = sample_data,
verbose = FALSE,
warmup = 500,
iter = 1000,
cores = 4
)
saveRDS(model_NormalMedia,"Recursos/Día2/Sesion1/0Recursos/Normal/model_NormalMedia2.rds")
model_NormalMedia <-
readRDS("Recursos/Día2/Sesion1/0Recursos/Normal/model_NormalMedia2.rds")La estimación del parámetro \(\theta\) y \(\sigma^2\) es:
tabla_Nor2 <- summary(model_NormalMedia,
pars = c("theta", "sigma2", "sigma"))$summary
tabla_Nor2 %>% tba()| mean | se_mean | sd | 2.5% | 25% | 50% | 75% | 97.5% | n_eff | Rhat | |
|---|---|---|---|---|---|---|---|---|---|---|
| theta | 9.0991 | 3e-04 | 0.0099 | 9.0801 | 9.0924 | 9.0989 | 9.1057 | 9.1189 | 1569.114 | 1.0002 |
| sigma2 | 0.6318 | 2e-04 | 0.0108 | 0.6101 | 0.6244 | 0.6314 | 0.6392 | 0.6531 | 1935.498 | 0.9991 |
| sigma | 0.7948 | 2e-04 | 0.0068 | 0.7811 | 0.7902 | 0.7946 | 0.7995 | 0.8081 | 1935.196 | 0.9991 |
posterior_theta <- as.array(model_NormalMedia, pars = "theta")
(mcmc_dens_chains(posterior_theta) +
mcmc_areas(posterior_theta) ) /
mcmc_trace(posterior_theta)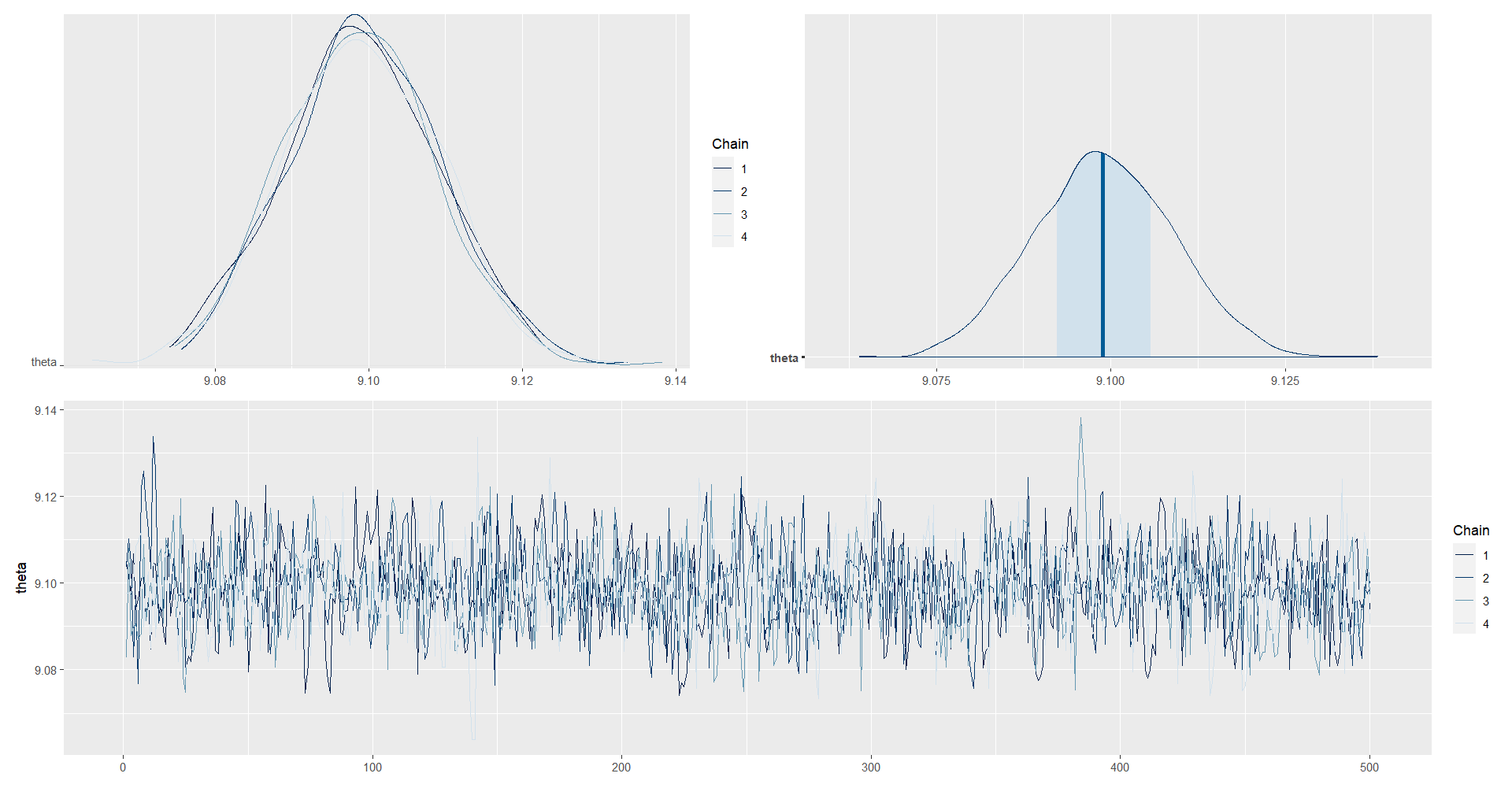
posterior_sigma2 <- as.array(model_NormalMedia, pars = "sigma2")
(mcmc_dens_chains(posterior_sigma2) +
mcmc_areas(posterior_sigma2) ) /
mcmc_trace(posterior_sigma2)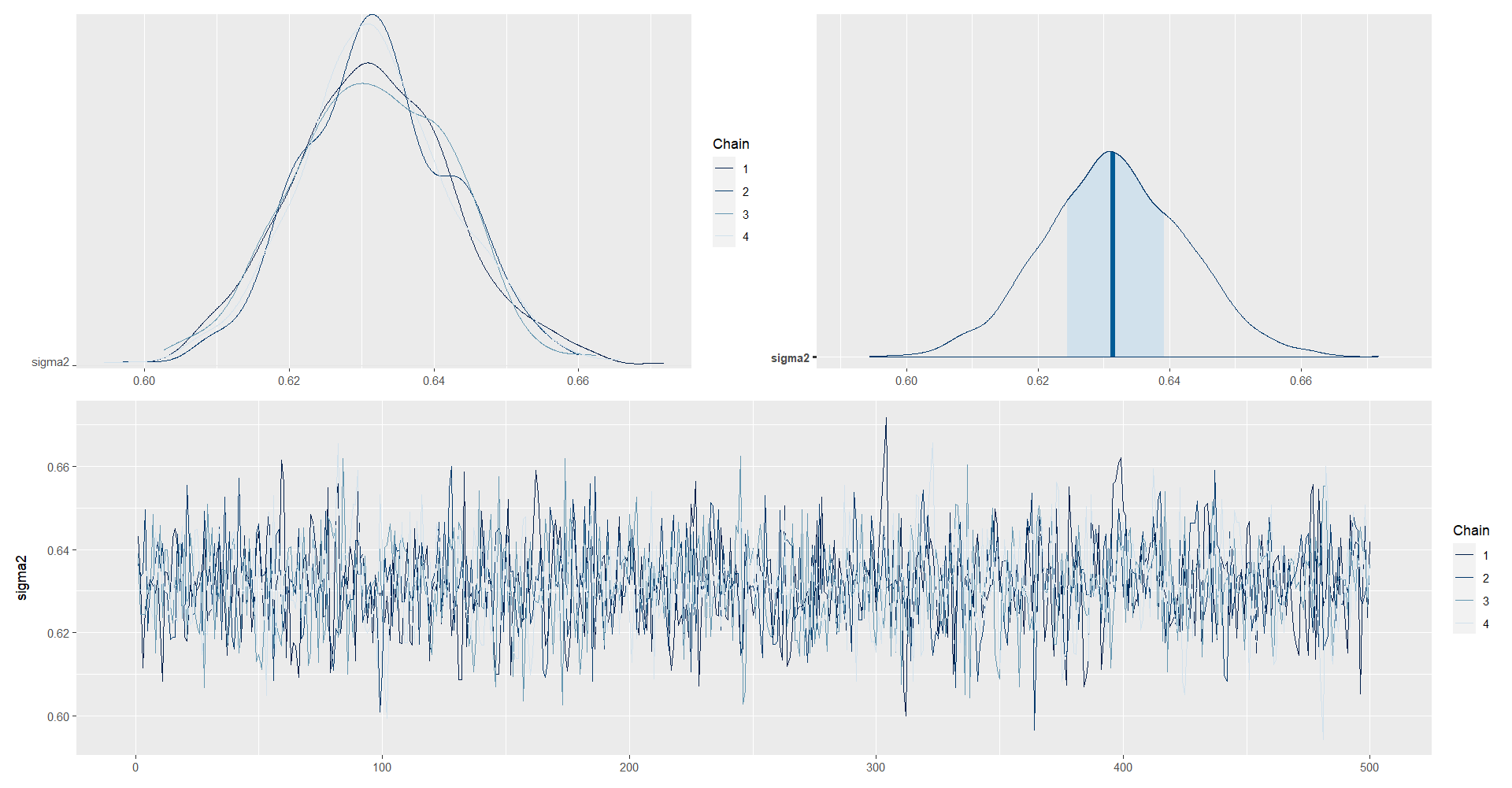
posterior_sigma <- as.array(model_NormalMedia, pars = "sigma")
(mcmc_dens_chains(posterior_sigma) +
mcmc_areas(posterior_sigma) ) /
mcmc_trace(posterior_sigma)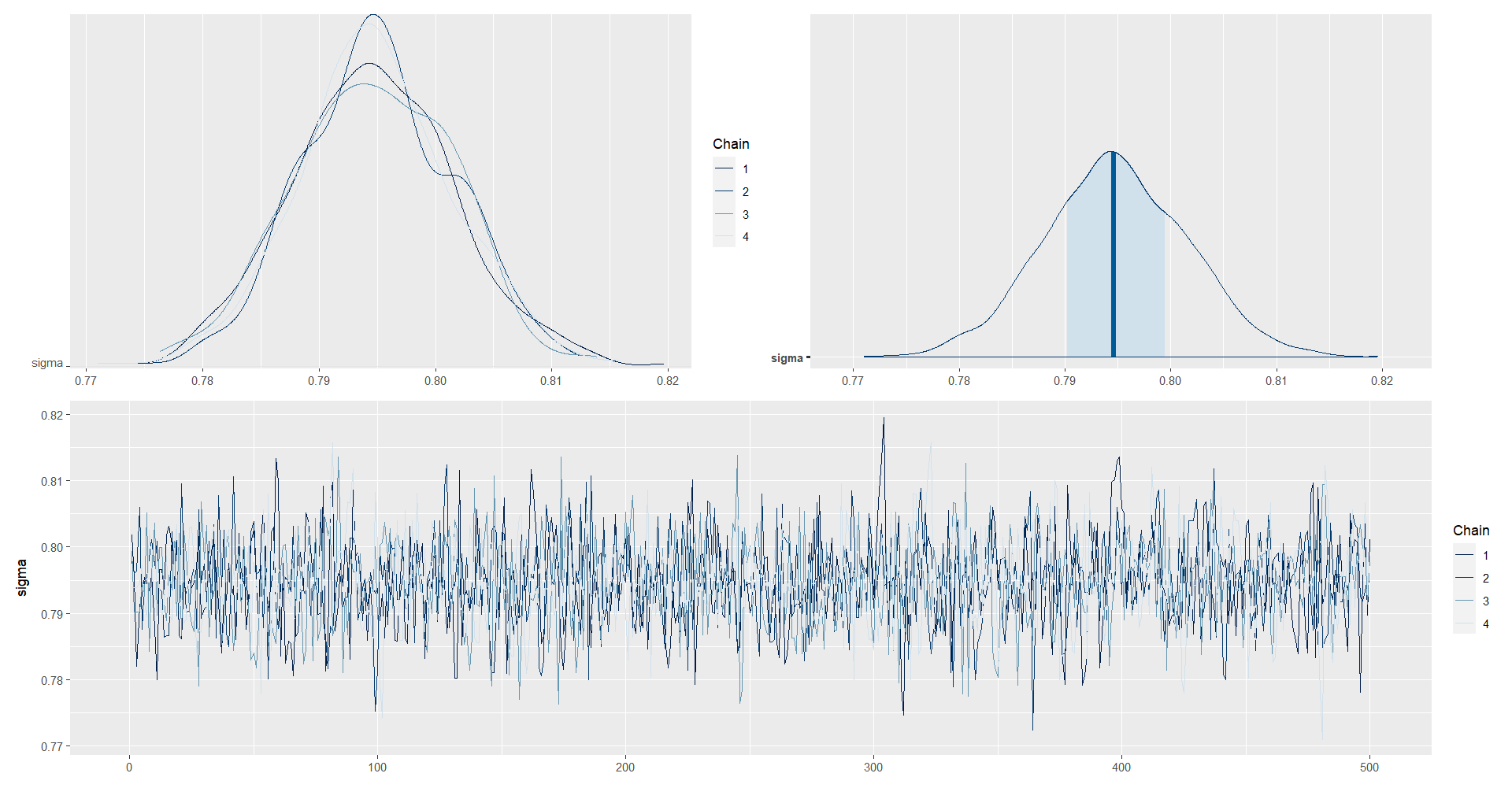
y_pred_B <- as.array(model_NormalMedia, pars = "ypred") %>%
as_draws_matrix()
rowsrandom <- sample(nrow(y_pred_B), 100)
y_pred2 <- y_pred_B[rowsrandom, ]
ppc_dens_overlay(y = as.numeric(exp(dataNormal$logIngreso)-1), y_pred2) + xlim(0,240000)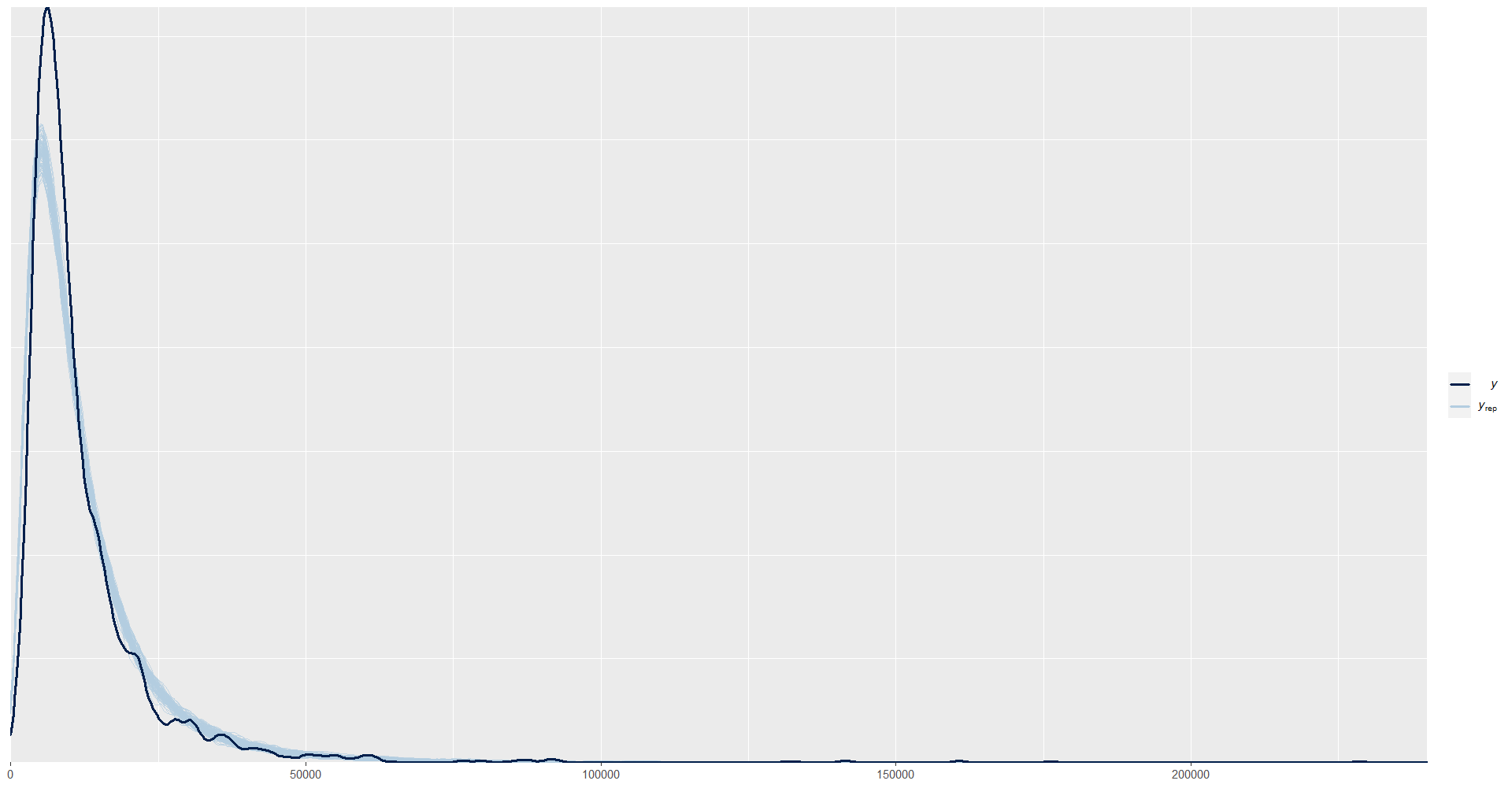
5.4.2 Modelo Multinomial
En esta sección discutimos el modelamiento bayesiano de datos provenientes de una distribución multinomial que corresponde a una extensión multivariada de la distribución binomial. Suponga que \(\textbf{Y}=(Y_1,\ldots,Y_p)'\) es un vector aleatorio con distribución multinomial, así, su distribución está parametrizada por el vector \(\boldsymbol{\theta}=(\theta_1,\ldots,\theta_p)'\) y está dada por la siguiente expresión
\[ \begin{equation} p(\mathbf{Y} \mid \boldsymbol{\theta})=\binom{n}{y_1,\ldots,y_p}\prod_{i=1}^p\theta_i^{y_i} \ \ \ \ \ \theta_i>0 \texttt{ , } \sum_{i=1}^py_i=n \texttt{ y } \sum_{i=1}^p\theta_i=1 \end{equation} \] Donde
\[ \begin{equation*} \binom{n}{y_1,\ldots,y_p}=\frac{n!}{y_1!\cdots y_p!}. \end{equation*} \]
Como cada parámetro \(\theta_i\) está restringido al espacio \(\Theta=[0,1]\), entonces es posible asignar a la distribución de Dirichlet como la distribución previa del vector de parámetros. Por lo tanto la distribución previa del vector de parámetros \(\boldsymbol{\theta}\), parametrizada por el vector de hiperparámetros \(\boldsymbol{\alpha}=(\alpha_1,\ldots,\alpha_p)'\), está dada por
\[ \begin{equation} p(\boldsymbol{\theta} \mid \boldsymbol{\alpha})=\frac{\Gamma(\alpha_1+\cdots+\alpha_p)}{\Gamma(\alpha_1)\cdots\Gamma(\alpha_p)} \prod_{i=1}^p\theta_i^{\alpha_i-1} \ \ \ \ \ \alpha_i>0 \texttt{ y } \sum_{i=1}^p\theta_i=1 \end{equation} \]
La distribución posterior del parámetro \(\boldsymbol{\theta}\) sigue una distribución \(Dirichlet(y_1+\alpha_1,\ldots,y_p+\alpha_p)\)
Obejtivo
Sea \(N_1\) el número de personas ocupadas, \(N_2\) Número de personas desocupadas, \(N_3\) es el número de personas inactivas en la población y \(N = N_1 +N_2 + N_3\). Entonces el objetivo es estimar el vector de parámetros \(\boldsymbol{P}=\left(P_{1},P_{2},P_{3}\right)\), con \(P_{k}=\frac{N_{k}}{N}\), para \(k=1,2,3\),
El estimador de \(\boldsymbol{P}\) esta dado por \[ \hat{\boldsymbol{P}} =\left(\hat{P}_{1},\hat{P}_{2},\hat{P}_{3}\right) \] donde, \[ \hat{P}_{k} = \frac{\sum_{s}w_{i}y_{ik}}{\sum_s{w_i}} = \frac{\hat{N}_k}{\hat{N}} \] y \(y_{ik}\) toma el valor 1 cuando la \(i-ésima\) persona responde la \(k-ésima\) categoría (Ocupado o Desocupado o Inactivo). Además, obtener \(\widehat{Var}\left(\hat{P}_{k}\right)\).
5.4.2.1 Práctica en STAN
Sea \(Y\) condición de actividad laboral
dataMult <- encuesta %>% filter(condact3 %in% 1:3) %>%
transmute(
empleo = as_factor(condact3)) %>%
group_by(empleo) %>% tally() %>%
mutate(theta = n/sum(n))
tba(dataMult)| empleo | n | theta |
|---|---|---|
| Ocupado | 33047 | 0.5267 |
| Desocupado | 2371 | 0.0378 |
| Inactivo | 27324 | 0.4355 |
donde 1 corresponde a Ocupado, 2 son los Desocupado y 3 son Inactivo
Creando código de STAN
data {
int<lower=0> k; // Número de cátegoria
int y[k]; // Número de exitos
vector[k] alpha; // Parámetro de las distribción previa
}
parameters {
simplex[k] theta;
}
transformed parameters {
real delta; // Tasa de desocupación
delta = theta[2]/ (theta[2] + theta[1]); // (Desocupado)/(Desocupado + Ocupado)
}
model {
y ~ multinomial(theta);
theta ~ dirichlet(alpha);
}
generated quantities {
int ypred[k];
ypred = multinomial_rng(theta, sum(y));
}Preparando el código de STAN
Multinom <- "Recursos/Día2/Sesion1/Data/modelosStan/6Multinom.stan" Organizando datos para STAN
sample_data <- list(k = nrow(dataMult),
y = dataMult$n,
alpha = c(0.5, 0.5, 0.5))Para ejecutar STAN en R tenemos la librería rstan
options(mc.cores = parallel::detectCores())
model_Multinom <- stan(
file = Multinom,
data = sample_data,
verbose = FALSE,
warmup = 500,
iter = 1000,
cores = 4
)
saveRDS(model_Multinom, "Recursos/Día2/Sesion1/0Recursos/Multinomial/model_Multinom.rds")
model_Multinom <- readRDS("Recursos/Día2/Sesion1/0Recursos/Multinomial/model_Multinom.rds")La estimación del parámetro \(\theta\) y \(\delta\) es:
tabla_Mul1 <- summary(model_Multinom, pars = c("delta", "theta"))$summary
tabla_Mul1 %>% tba()| mean | se_mean | sd | 2.5% | 25% | 50% | 75% | 97.5% | n_eff | Rhat | |
|---|---|---|---|---|---|---|---|---|---|---|
| delta | 0.0670 | 0 | 0.0013 | 0.0644 | 0.0661 | 0.0670 | 0.0679 | 0.0695 | 1414.051 | 1.0014 |
| theta[1] | 0.5268 | 0 | 0.0019 | 0.5231 | 0.5255 | 0.5268 | 0.5280 | 0.5305 | 1692.834 | 0.9989 |
| theta[2] | 0.0378 | 0 | 0.0008 | 0.0363 | 0.0373 | 0.0378 | 0.0383 | 0.0393 | 1379.738 | 1.0018 |
| theta[3] | 0.4354 | 0 | 0.0019 | 0.4317 | 0.4341 | 0.4354 | 0.4367 | 0.4392 | 1633.676 | 0.9997 |
posterior_theta1 <- as.array(model_Multinom, pars = "theta[1]")
(mcmc_dens_chains(posterior_theta1) +
mcmc_areas(posterior_theta1) ) /
mcmc_trace(posterior_theta1)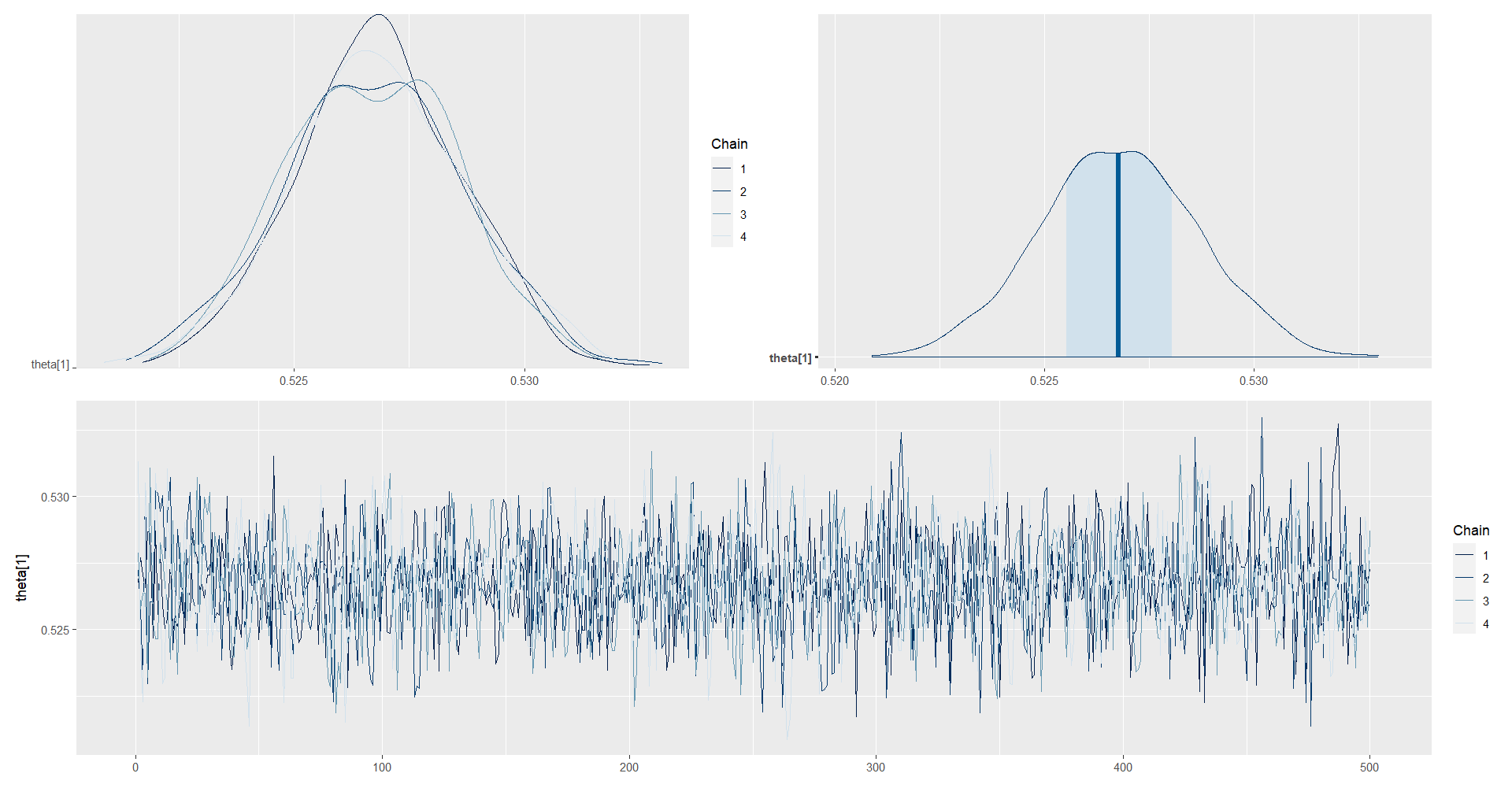
posterior_theta2 <- as.array(model_Multinom, pars = "theta[2]")
(mcmc_dens_chains(posterior_theta2) +
mcmc_areas(posterior_theta2) ) /
mcmc_trace(posterior_theta2)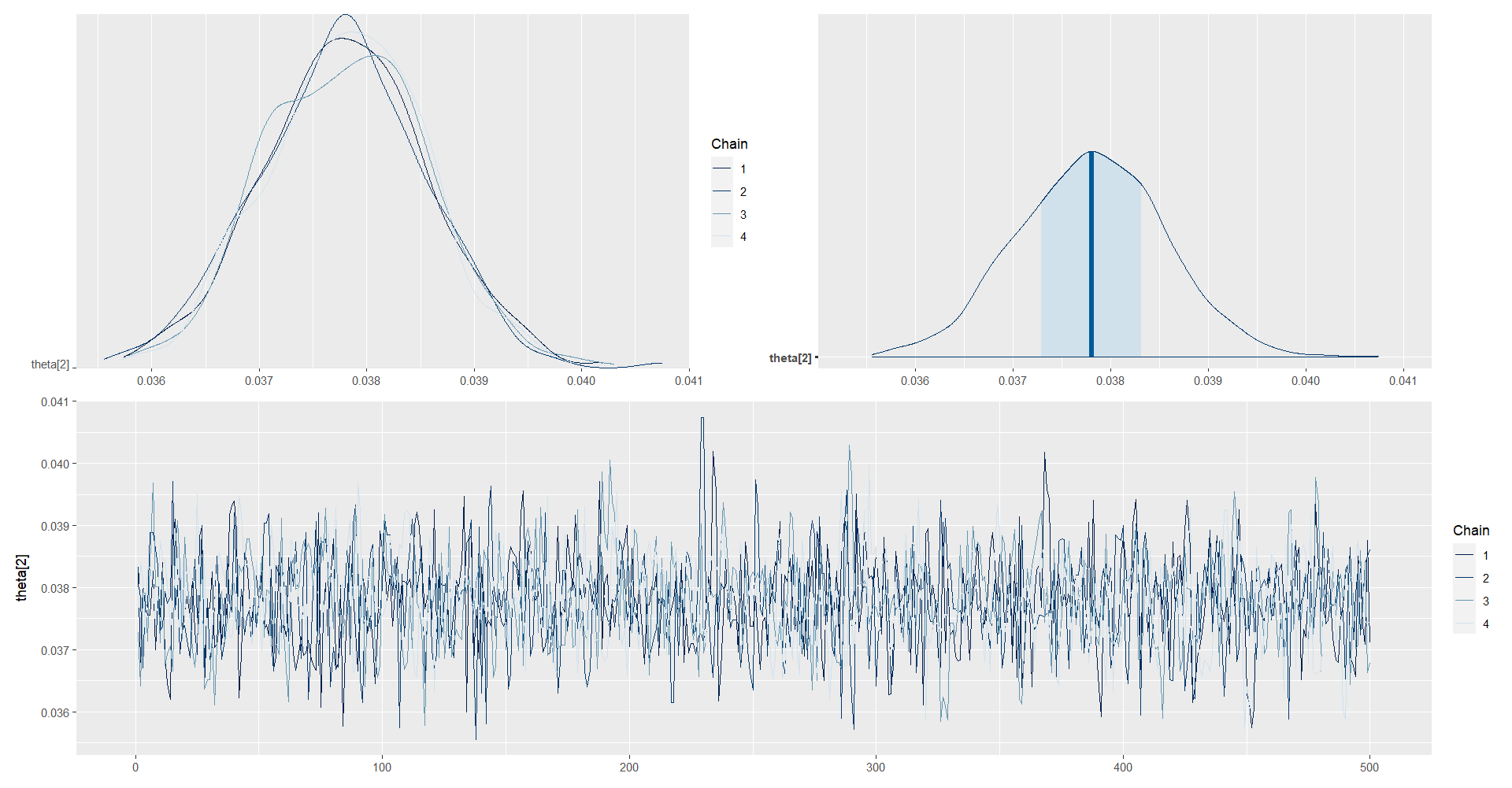
posterior_theta3 <- as.array(model_Multinom, pars = "theta[3]")
(mcmc_dens_chains(posterior_theta3) +
mcmc_areas(posterior_theta3) ) /
mcmc_trace(posterior_theta3)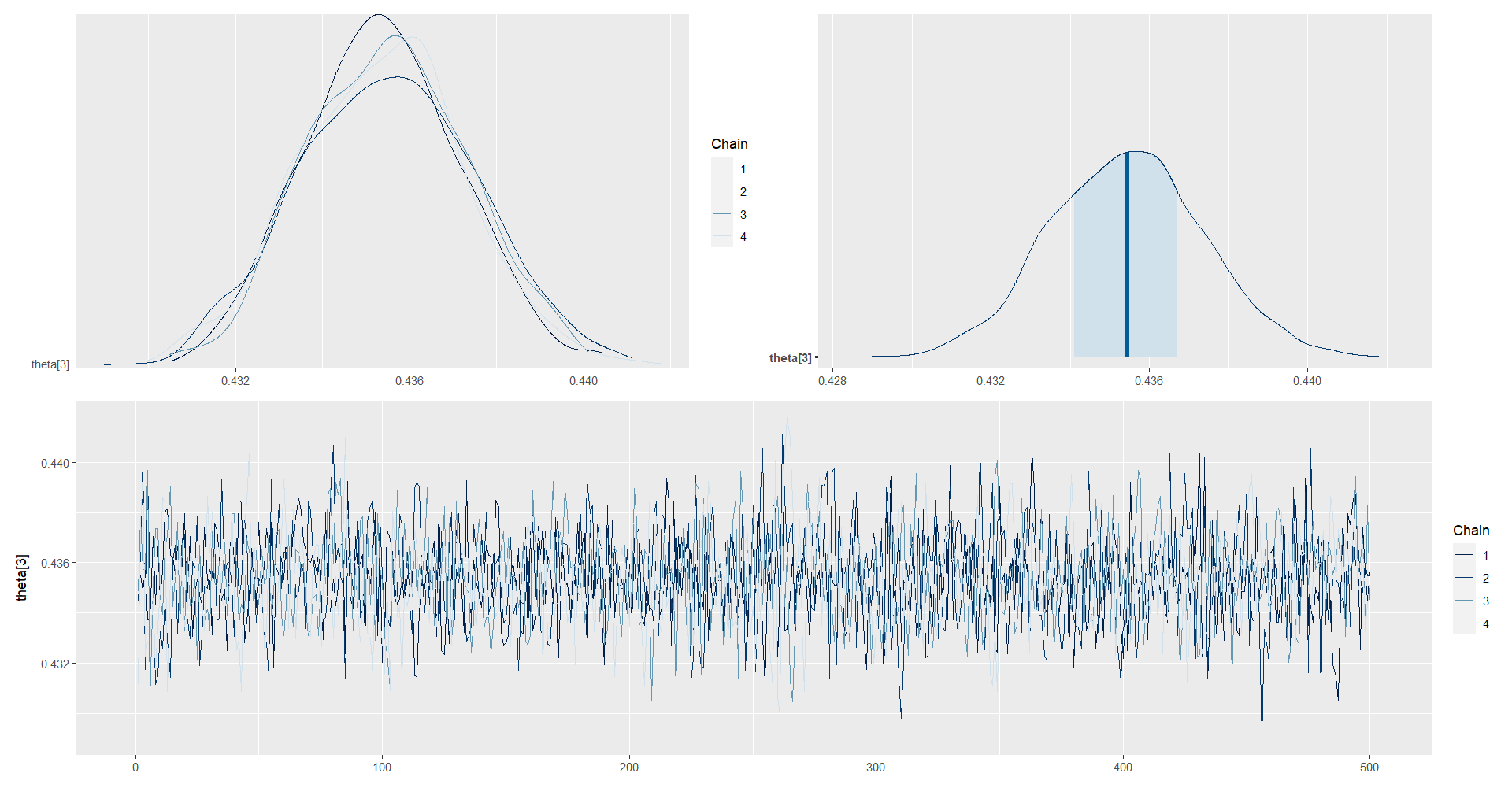
posterior_delta <- as.array(model_Multinom, pars = "delta")
(mcmc_dens_chains(posterior_delta) +
mcmc_areas(posterior_delta) ) /
mcmc_trace(posterior_delta)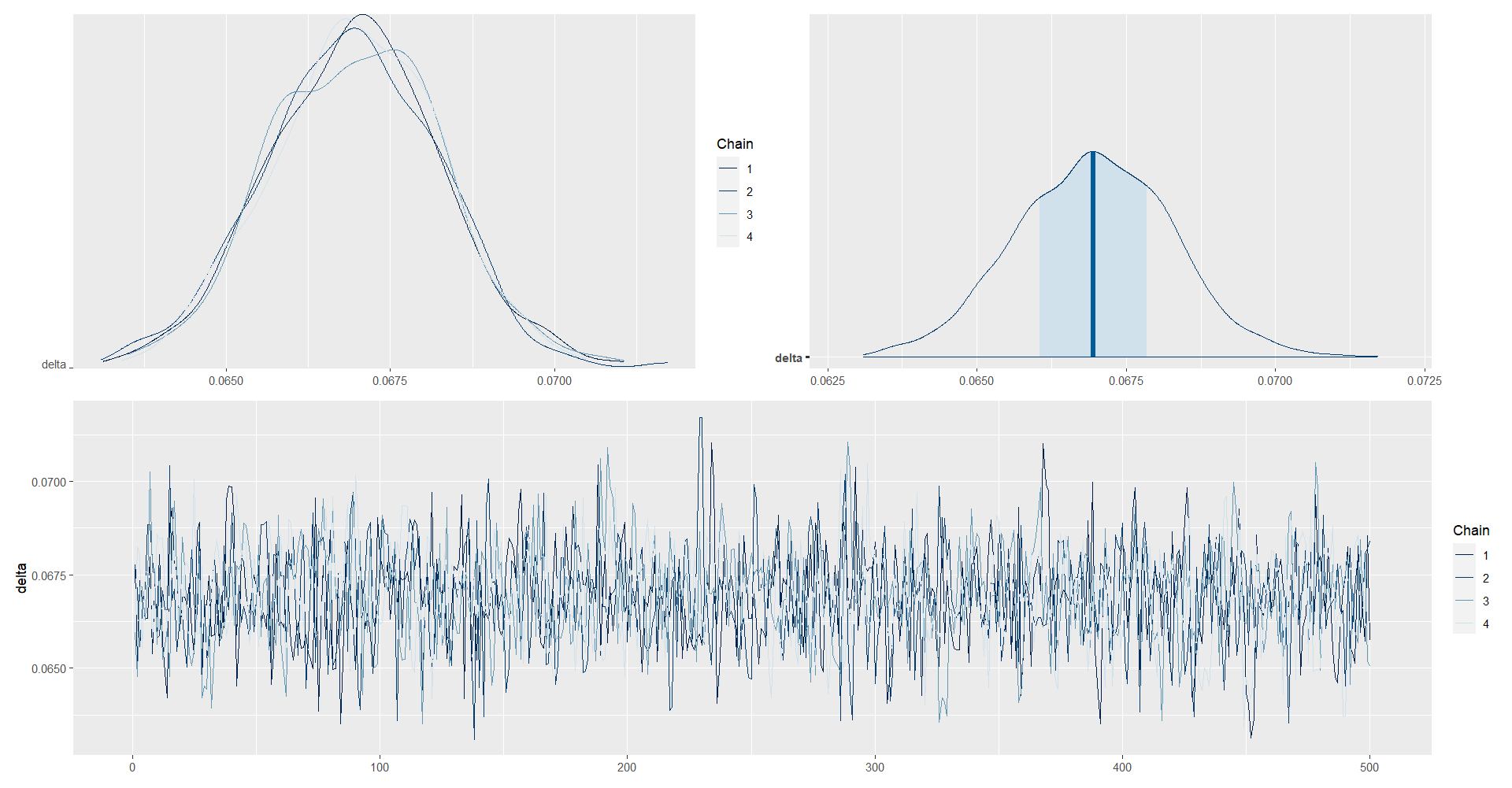
La imagen es muy pesada no se carga al repositorio.
n <- nrow(dataMult)
y_pred_B <- as.array(model_Multinom, pars = "ypred") %>%
as_draws_matrix()
rowsrandom <- sample(nrow(y_pred_B), 100)
y_pred2 <- y_pred_B[rowsrandom, 1:n]
ppc_dens_overlay(y = as.numeric(dataMult$n), y_pred2)