8.2 Preparando los insumos para STAN
- Dividir la base de datos en dominios observados y no observados
Dominios observados.
data_dir <- base_FH %>% filter(!is.na(T_pobreza))Dominios NO observados.
data_syn <-
base_FH %>% anti_join(data_dir %>% select(dam2))
tba(data_syn[,1:8] %>% slice(1:10))| dam2 | pobreza | T_pobreza | n_effec | varhat | modificacion_humana | accesibilidad_hospitales | accesibilidad_hosp_caminado |
|---|---|---|---|---|---|---|---|
| 00202 | NA | NA | NA | NA | -0.3758 | 0.0000 | 0.1482 |
| 00203 | NA | NA | NA | NA | -0.9259 | 0.5732 | -0.1402 |
| 00204 | NA | NA | NA | NA | -1.3166 | 1.1111 | 0.4438 |
| 00205 | NA | NA | NA | NA | -0.7474 | 2.1155 | 1.2271 |
| 00207 | NA | NA | NA | NA | 1.7368 | -0.7648 | -0.4861 |
| 00208 | NA | NA | NA | NA | -0.5942 | 0.3212 | -0.1697 |
| 00209 | NA | NA | NA | NA | -1.5280 | 3.0192 | 1.9428 |
| 00210 | NA | NA | NA | NA | -1.0038 | 0.5778 | 0.2678 |
| 00305 | NA | NA | NA | NA | -0.8480 | 1.5047 | 3.2004 |
| 00404 | NA | NA | NA | NA | -0.5678 | 1.0735 | 0.9856 |
- Definir matriz de efectos fijos.
## Dominios observados
Xdat <- cbind(inter = 1,data_dir[,names_cov])
## Dominios no observados
Xs <- cbind(inter = 1,data_syn[,names_cov])- Creando lista de parámetros para
STAN
sample_data <- list(
N1 = nrow(Xdat), # Observados.
N2 = nrow(Xs), # NO Observados.
p = ncol(Xdat), # Número de regresores.
X = as.matrix(Xdat), # Covariables Observados.
Xs = as.matrix(Xs), # Covariables NO Observados
y = as.numeric(data_dir$T_pobreza),
sigma_e = sqrt(data_dir$varhat)
)- Compilando el modelo en
STAN
library(rstan)
fit_FH_arcoseno <- "Recursos/Día3/Sesion1/Data/modelosStan/15FH_arcsin_normal.stan"
options(mc.cores = parallel::detectCores())
model_FH_arcoseno <- stan(
file = fit_FH_arcoseno,
data = sample_data,
verbose = FALSE,
warmup = 500,
iter = 1000,
cores = 4
)
saveRDS(model_FH_arcoseno,
"Recursos/Día3/Sesion1/Data/model_FH_arcoseno.rds")model_FH_arcoseno <- readRDS("Recursos/Día3/Sesion1/Data/model_FH_arcoseno.rds")8.2.1 Resultados del modelo para los dominios observados.
En este código, se cargan las librerías bayesplot, posterior y patchwork, que se utilizan para realizar gráficos y visualizaciones de los resultados del modelo.
A continuación, se utiliza la función as.array() y as_draws_matrix() para extraer las muestras de la distribución posterior del parámetro theta del modelo, y se seleccionan aleatoriamente 100 filas de estas muestras utilizando la función sample(), lo que resulta en la matriz y_pred2.
Finalmente, se utiliza la función ppc_dens_overlay() de bayesplot para graficar una comparación entre la distribución empírica de la variable observada pobreza en los datos (data_dir$pobreza) y las distribuciones predictivas posteriores simuladas para la misma variable (y_pred2). La función ppc_dens_overlay() produce un gráfico de densidad para ambas distribuciones, lo que permite visualizar cómo se comparan.
library(bayesplot)
library(patchwork)
library(posterior)
y_pred_B <- as.array(model_FH_arcoseno, pars = "theta") %>%
as_draws_matrix()
rowsrandom <- sample(nrow(y_pred_B), 100)
y_pred2 <- y_pred_B[rowsrandom, ]
ppc_dens_overlay(y = as.numeric(data_dir$pobreza), y_pred2)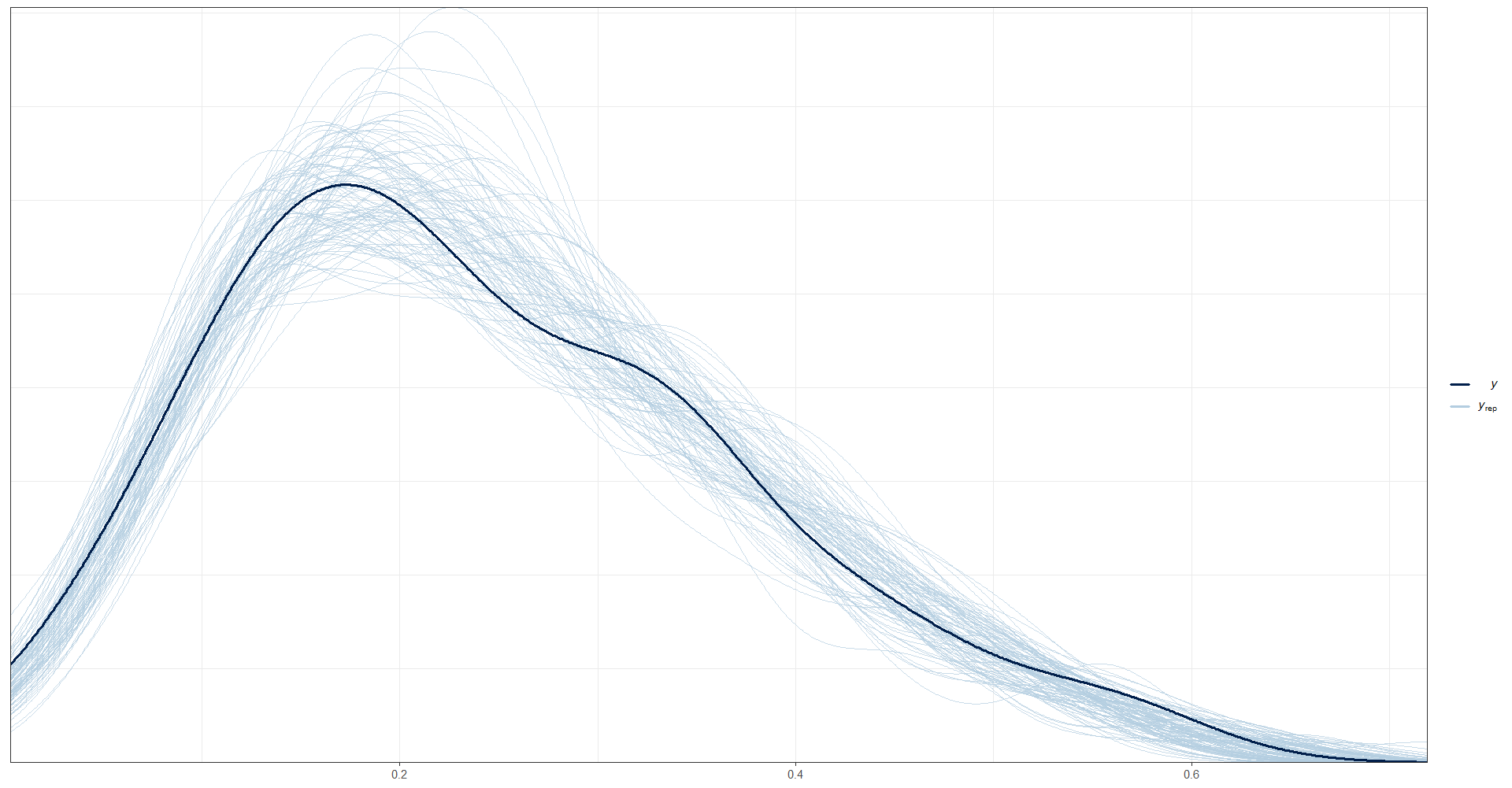
Análisis gráfico de la convergencia de las cadenas de \(\sigma^2_u\).
posterior_sigma2_u <- as.array(model_FH_arcoseno, pars = "sigma2_u")
(mcmc_dens_chains(posterior_sigma2_u) +
mcmc_areas(posterior_sigma2_u) ) /
mcmc_trace(posterior_sigma2_u)
# traceplot(model_FH_arcoseno,pars = "sigma2_u",inc_warmup = TRUE)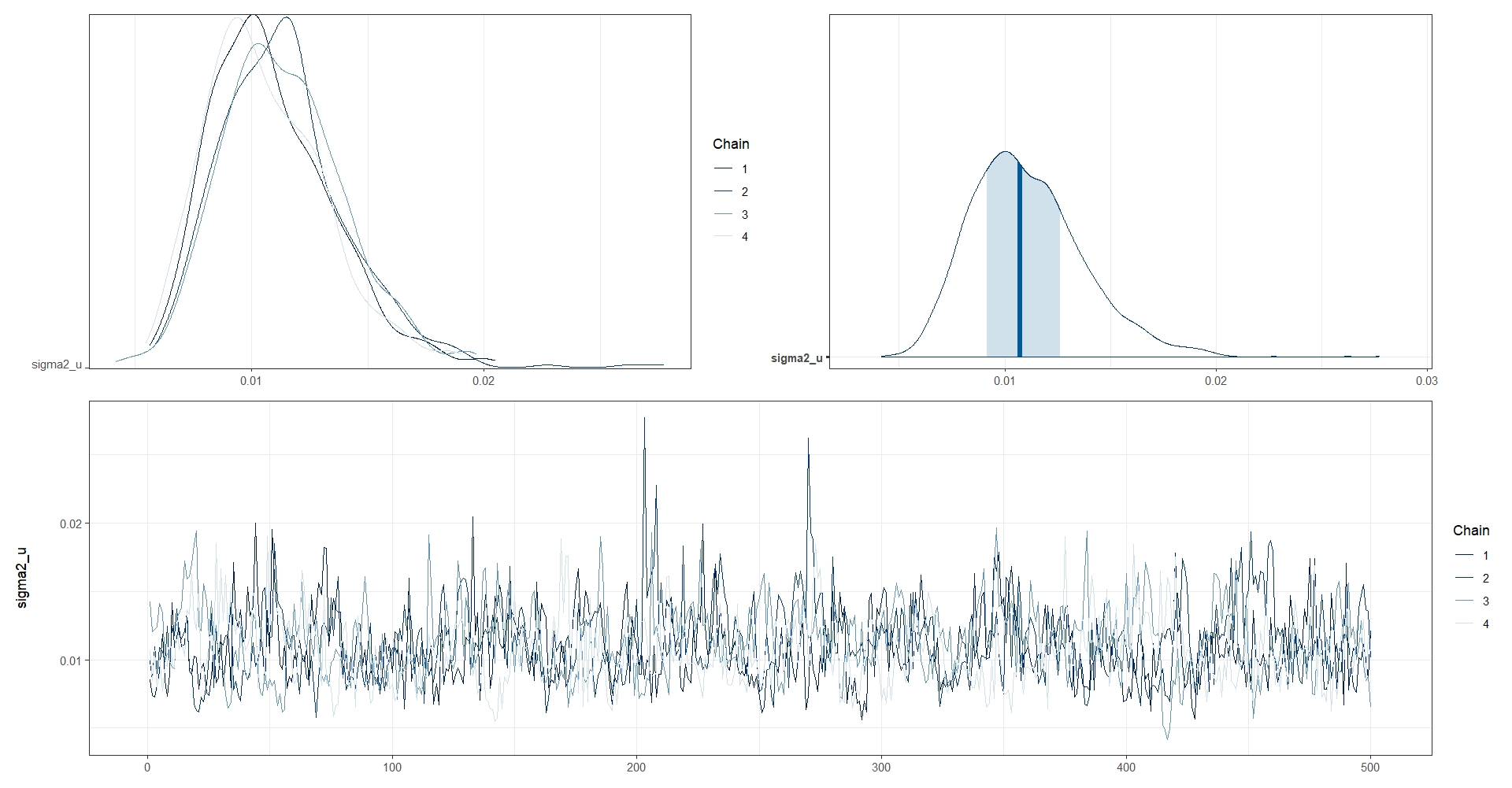
Estimación del FH de la pobreza en los dominios observados.
theta_FH <- summary(model_FH_arcoseno,pars = "theta")$summary %>%
data.frame()
data_dir %<>% mutate(pred_arcoseno = theta_FH$mean,
pred_arcoseno_EE = theta_FH$sd,
Cv_pred = pred_arcoseno_EE/pred_arcoseno)Estimación del FH de la pobreza en los dominios NO observados.
theta_FH_pred <- summary(model_FH_arcoseno,pars = "theta_pred")$summary %>%
data.frame()
data_syn <- data_syn %>%
mutate(pred_arcoseno = theta_FH_pred$mean,
pred_arcoseno_EE = theta_FH_pred$sd,
Cv_pred = pred_arcoseno_EE/pred_arcoseno)