7.2 Preparando los insumos para STAN | Desagregación de datos en encuestas de hogares: metodologías bayesianas para modelos de estimación en áreas pequeñas

7.2 Preparando los insumos para `STAN`

Dividir la base de datos en dominios observados y no observados.

Dominios observados.

data_dir <- base_FH %>% filter(!is.na(pobreza))

Dominios NO observados.

data_syn <-
  base_FH %>% anti_join(data_dir %>% select(dam2))
tba(data_syn[1:10,1:8])

dam2	nd	pobreza	vardir	hat_var	modificacion_humana	accesibilidad_hospitales	accesibilidad_hosp_caminado
00202	NA	NA	NA	NA	-0.3758	0.0000	0.1482
00203	NA	NA	NA	NA	-0.9259	0.5732	-0.1402
00204	NA	NA	NA	NA	-1.3166	1.1111	0.4438
00205	NA	NA	NA	NA	-0.7474	2.1155	1.2271
00207	NA	NA	NA	NA	1.7368	-0.7648	-0.4861
00208	NA	NA	NA	NA	-0.5942	0.3212	-0.1697
00209	NA	NA	NA	NA	-1.5280	3.0192	1.9428
00210	NA	NA	NA	NA	-1.0038	0.5778	0.2678
00305	NA	NA	NA	NA	-0.8480	1.5047	3.2004
00404	NA	NA	NA	NA	-0.5678	1.0735	0.9856

Definir matriz de efectos fijos.

Define un modelo lineal utilizando la función formula(), que incluye varias variables predictoras, como la edad, la etnia, la tasa de desocupación, entre otras.

Utiliza la función model.matrix() para generar matrices de diseño (Xdat y Xs) a partir de los datos observados (data_dir) y no observados (data_syn) para utilizar en la construcción de modelos de regresión. La función model.matrix() convierte las variables categóricas en variables binarias (dummy), de manera que puedan ser utilizadas.

formula_mod  <- formula(~ sexo2 + 
                         anoest2 +
                         anoest3 +
                         anoest4 + 
                         edad2 +
                         edad3  +
                         edad4  +
                         edad5 +
                         tasa_desocupacion +
                         luces_nocturnas +
                         cubrimiento_cultivo +
                         alfabeta)
## Dominios observados
Xdat <- model.matrix(formula_mod, data = data_dir)

## Dominios no observados
Xs <- model.matrix(formula_mod, data = data_syn)

Ahora, se utiliza la función setdiff() para identificar las columnas de Xdat que no están presentes en $X_s$, es decir, las variables que no se encuentran en los datos no observados. A continuación, se crea una matriz temporal (temp) con ceros para las columnas faltantes de $X_s$, y se agregan estas columnas a $X_s$ utilizando cbind(). El resultado final es una matriz Xs con las mismas variables que Xdat, lo que asegura que se puedan realizar comparaciones adecuadas entre los datos observados y no observados en la construcción de modelos de regresión. En general, este código es útil para preparar los datos para su posterior análisis y asegurar que los modelos de regresión sean adecuados para su uso.

temp <- setdiff(colnames(Xdat),colnames(Xs))

temp <- matrix(
  0,
  nrow = nrow(Xs),
  ncol = length(temp),
  dimnames = list(1:nrow(Xs), temp)
)

Xs <- cbind(Xs,temp)[,colnames(Xdat)]

Creando lista de parámetros para STAN

sample_data <- list(
  N1 = nrow(Xdat),   # Observados.
  N2 = nrow(Xs),   # NO Observados.
  p  = ncol(Xdat),       # Número de regresores.
  X  = as.matrix(Xdat),  # Covariables Observados.
  Xs = as.matrix(Xs),    # Covariables NO Observados
  y  = as.numeric(data_dir$pobreza), # Estimación directa
  sigma_e = sqrt(data_dir$hat_var)   # Error de estimación
)

Rutina implementada en STAN

data {
  int<lower=0> N1;   // number of data items
  int<lower=0> N2;   // number of data items for prediction
  int<lower=0> p;   // number of predictors
  matrix[N1, p] X;   // predictor matrix
  matrix[N2, p] Xs;   // predictor matrix
  vector[N1] y;      // predictor matrix 
  vector[N1] sigma_e; // known variances
}

parameters {
  vector[p] beta;       // coefficients for predictors
  real<lower=0> sigma2_u;
  vector[N1] u;
}

transformed parameters{
  vector[N1] theta;
  vector[N1] thetaSyn;
  vector[N1] thetaFH;
  vector[N1] gammaj;
  real<lower=0> sigma_u;
  thetaSyn = X * beta;
  theta = thetaSyn + u;
  sigma_u = sqrt(sigma2_u);
  gammaj =  to_vector(sigma_u ./ (sigma_u + sigma_e));
  thetaFH = (gammaj) .* y + (1-gammaj).*thetaSyn; 
}

model {
  // likelihood
  y ~ normal(theta, sigma_e); 
  // priors
  beta ~ normal(0, 100);
  u ~ normal(0, sigma_u);
  sigma2_u ~ inv_gamma(0.0001, 0.0001);
}

generated quantities{
  vector[N2] y_pred;
  for(j in 1:N2) {
    y_pred[j] = normal_rng(Xs[j] * beta, sigma_u);
  }
}

Compilando el modelo en STAN. A continuación mostramos la forma de compilar el código de STAN desde R.

En este código se utiliza la librería rstan para ajustar un modelo bayesiano utilizando el archivo 17FH_normal.stan que contiene el modelo escrito en el lenguaje de modelado probabilístico Stan.

En primer lugar, se utiliza la función stan() para ajustar el modelo a los datos de sample_data. Los argumentos que se pasan a stan() incluyen el archivo que contiene el modelo (fit_FH_normal), los datos (sample_data), y los argumentos para controlar el proceso de ajuste del modelo, como el número de iteraciones para el período de calentamiento (warmup) y el período de muestreo (iter), y el número de núcleos de la CPU para utilizar en el proceso de ajuste (cores).

Además, se utiliza la función parallel::detectCores() para detectar automáticamente el número de núcleos disponibles en la CPU, y se establece la opción mc.cores para aprovechar el número máximo de núcleos disponibles para el ajuste del modelo.

El resultado del ajuste del modelo es almacenado en model_FH_normal, que contiene una muestra de la distribución posterior del modelo, la cual puede ser utilizada para realizar inferencias sobre los parámetros del modelo y las predicciones. En general, este código es útil para ajustar modelos bayesianos utilizando Stan y realizar inferencias posteriores.

library(rstan)
fit_FH_normal <- "Recursos/Día2/Sesion3/Data/modelosStan/17FH_normal.stan"
options(mc.cores = parallel::detectCores())
model_FH_normal <- stan(
  file = fit_FH_normal,  
  data = sample_data,   
  verbose = FALSE,
  warmup = 500,         
  iter = 1000,            
  cores = 4              
)
saveRDS(object = model_FH_normal,
        file = "Recursos/Día2/Sesion3/Data/model_FH_normal.rds")

Leer el modelo

model_FH_normal<- readRDS("Recursos/Día2/Sesion3/Data/model_FH_normal.rds")

7.2.1 Resultados del modelo para los dominios observados.

En este código, se cargan las librerías bayesplot, posterior y patchwork, que se utilizan para realizar gráficos y visualizaciones de los resultados del modelo.

A continuación, se utiliza la función as.array() y as_draws_matrix() para extraer las muestras de la distribución posterior del parámetro theta del modelo, y se seleccionan aleatoriamente 100 filas de estas muestras utilizando la función sample(), lo que resulta en la matriz y_pred2.

Finalmente, se utiliza la función ppc_dens_overlay() de bayesplot para graficar una comparación entre la distribución empírica de la variable observada pobreza en los datos (data_dir$pobreza) y las distribuciones predictivas posteriores simuladas para la misma variable (y_pred2). La función ppc_dens_overlay() produce un gráfico de densidad para ambas distribuciones, lo que permite visualizar cómo se comparan.

library(bayesplot)
library(posterior)
library(patchwork)
y_pred_B <- as.array(model_FH_normal, pars = "theta") %>% 
  as_draws_matrix()
rowsrandom <- sample(nrow(y_pred_B), 100)
y_pred2 <- y_pred_B[rowsrandom, ]
ppc_dens_overlay(y = as.numeric(data_dir$pobreza), y_pred2)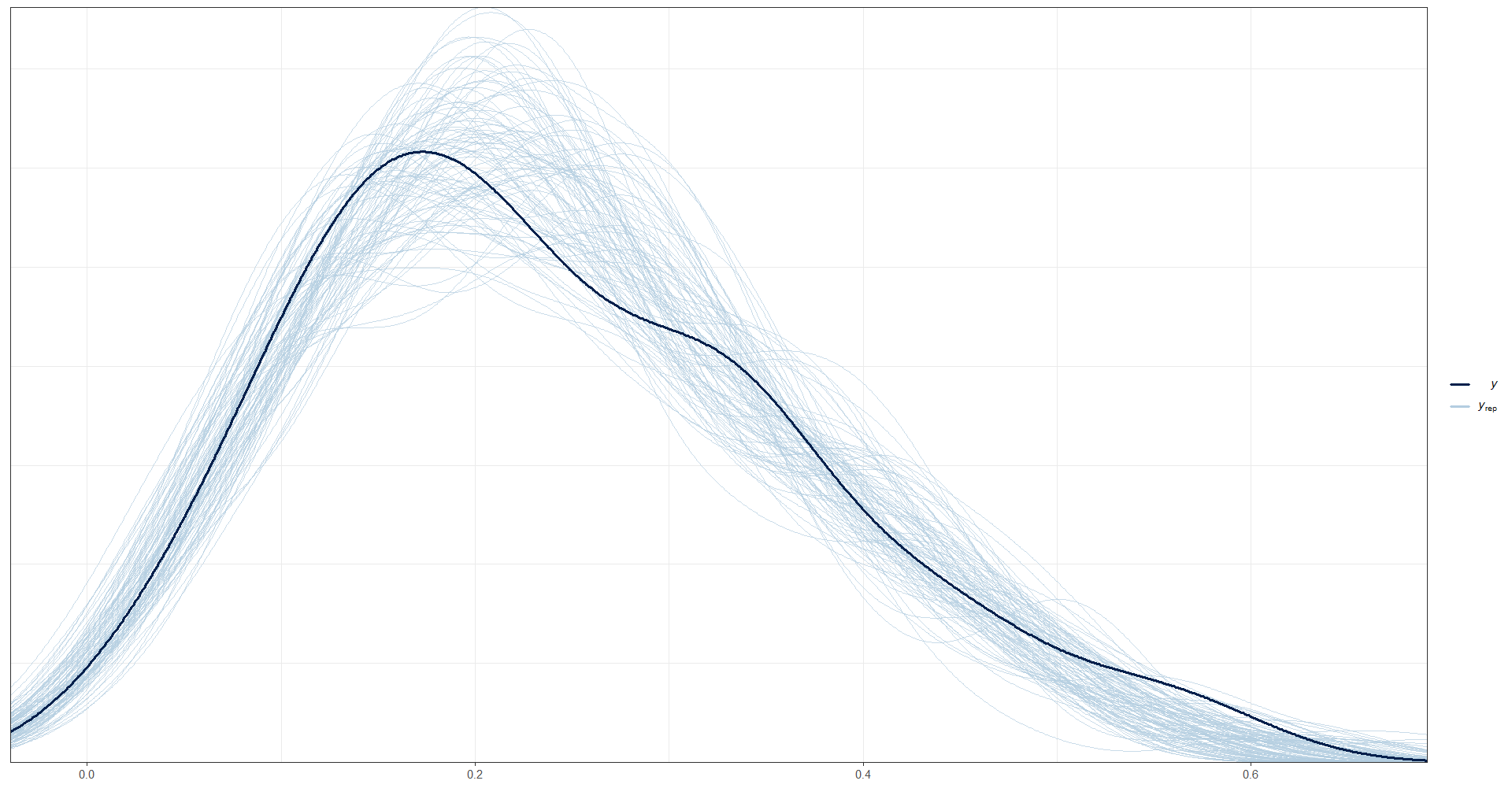

Análisis gráfico de la convergencia de las cadenas de $\sigma^2_V$.

posterior_sigma2_u <- as.array(model_FH_normal, pars = "sigma2_u")
(mcmc_dens_chains(posterior_sigma2_u) +
    mcmc_areas(posterior_sigma2_u) ) / 
  mcmc_trace(posterior_sigma2_u)
#traceplot(model_FH_normal, pars = "sigma2_u", inc_warmup = TRUE)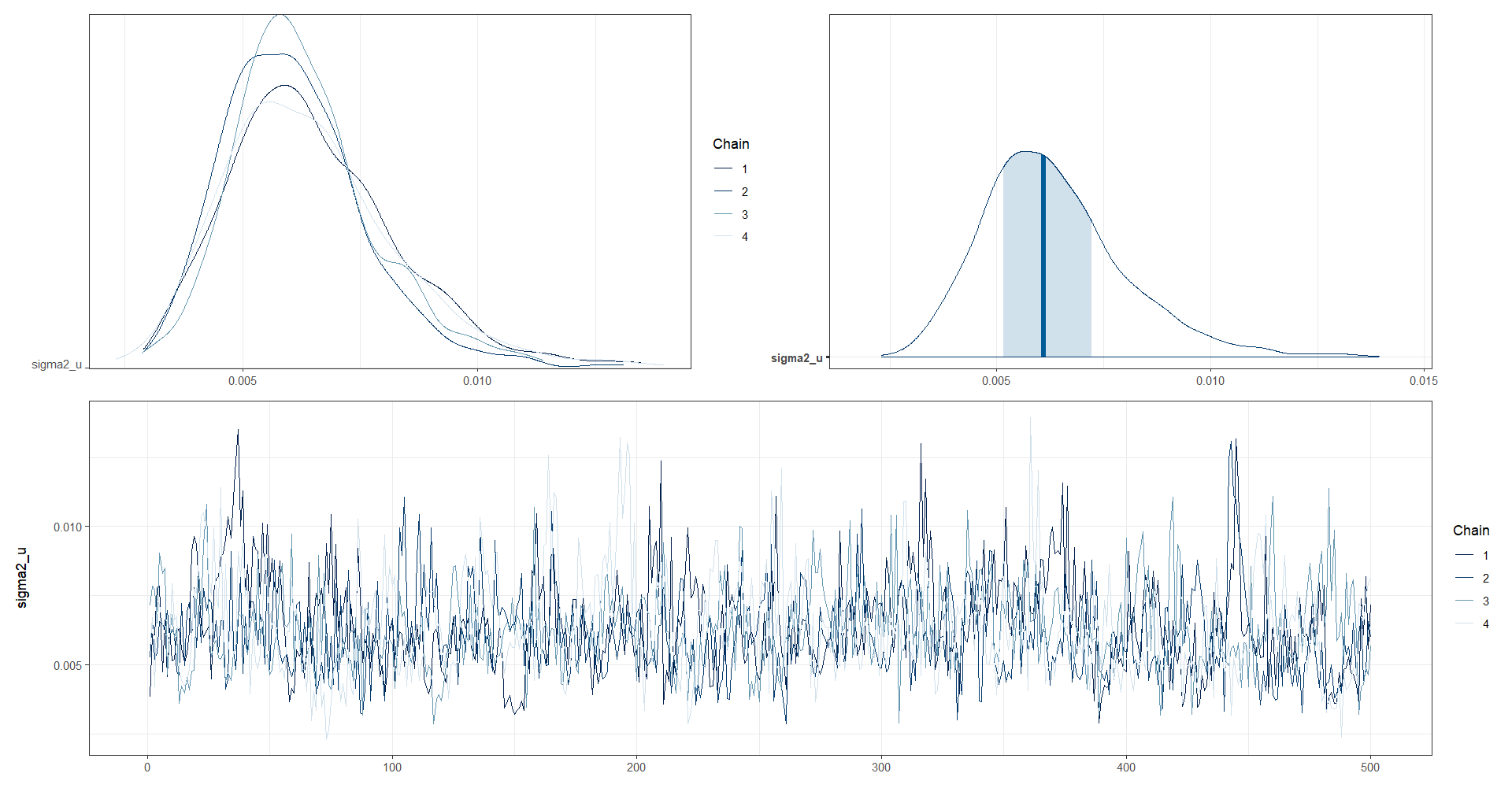

Como método de validación se comparan las diferentes elementos de la estimación del modelo de FH obtenidos en STAN

theta <-   summary(model_FH_normal,pars =  "theta")$summary %>%
  data.frame()
thetaSyn <-   summary(model_FH_normal,pars =  "thetaSyn")$summary %>%
  data.frame()
theta_FH <-   summary(model_FH_normal,pars =  "thetaFH")$summary %>%
  data.frame()

data_dir %<>% mutate(
            thetadir = pobreza,
            theta_pred = theta$mean,
            thetaSyn = thetaSyn$mean,
            thetaFH = theta_FH$mean,
            theta_pred_EE = theta$sd,
            Cv_theta_pred = theta_pred_EE/theta_pred
            ) 
# saveRDS(data_dir,"Recursos/Día2/Sesion3/0Recursos/data_dir.rds")
# Estimación predicción del modelo vs ecuación ponderada de FH 
p11 <- ggplot(data_dir, aes(x = theta_pred, y = thetaFH)) +
  geom_point() + 
  geom_abline(slope = 1,intercept = 0, colour = "red") +
  theme_bw(10) 

# Estimación con la ecuación ponderada de FH Vs estimación sintética
p12 <- ggplot(data_dir, aes(x = thetaSyn, y = thetaFH)) +
  geom_point() + 
  geom_abline(slope = 1,intercept = 0, colour = "red") +
  theme_bw(10) 

# Estimación con la ecuación ponderada de FH Vs estimación directa

p21 <- ggplot(data_dir, aes(x = thetadir, y = thetaFH)) +
  geom_point() + 
  geom_abline(slope = 1,intercept = 0, colour = "red") +
  theme_bw(10) 

# Estimación directa Vs estimación sintética

p22 <- ggplot(data_dir, aes(x = thetadir, y = thetaSyn)) +
  geom_point() + 
  geom_abline(slope = 1,intercept = 0, colour = "red") +
  theme_bw(10) 

(p11+p12)/(p21+p22)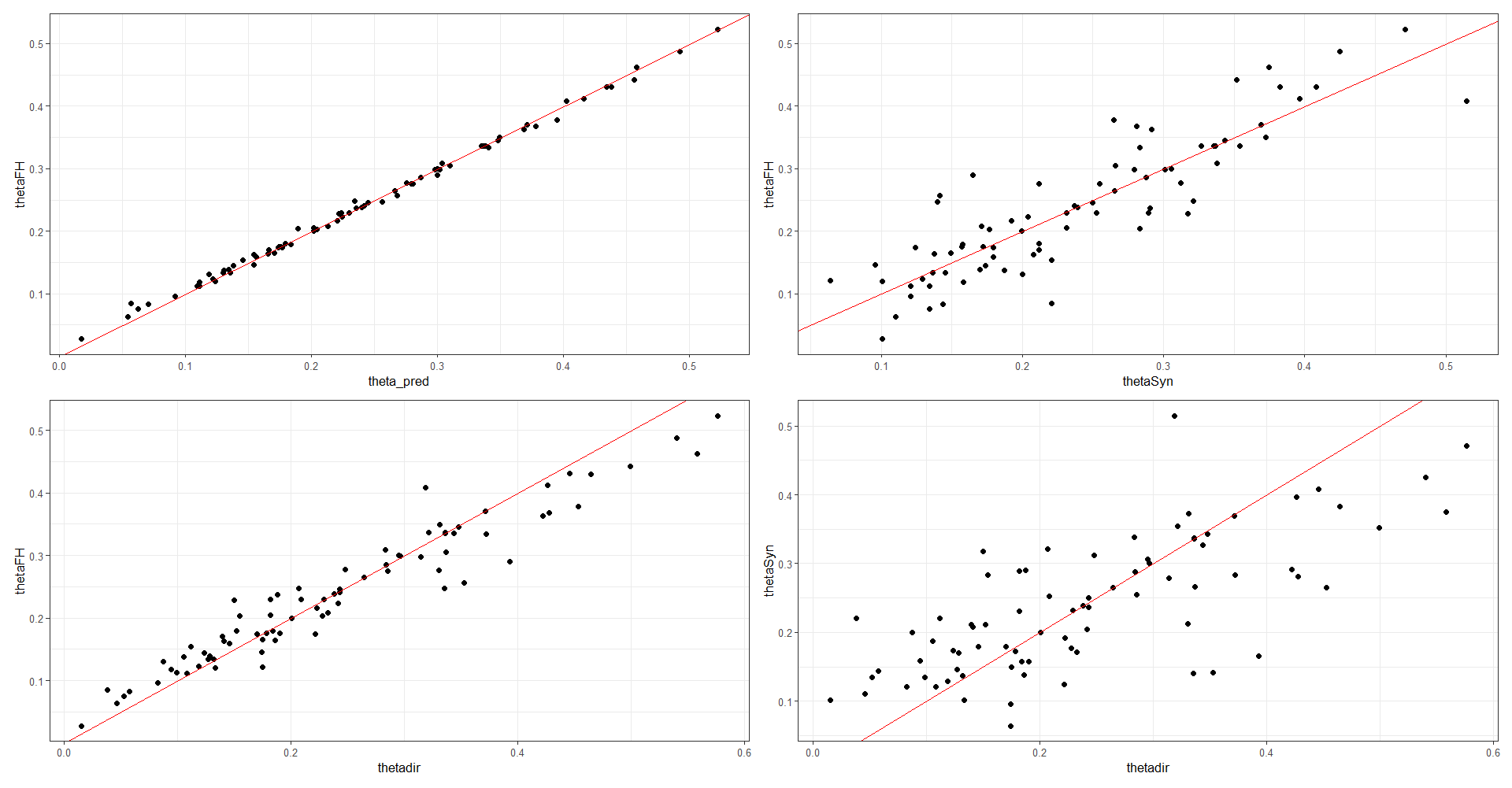

Estimación del FH de la pobreza en los dominios NO observados.

theta_syn_pred <- summary(model_FH_normal,pars =  "y_pred")$summary %>%
  data.frame()

data_syn <- data_syn %>% 
  mutate(
    theta_pred = theta_syn_pred$mean,
    thetaSyn = theta_pred,
    thetaFH = theta_pred,
    theta_pred_EE = theta_syn_pred$sd,
    Cv_theta_pred = theta_pred_EE/theta_pred)

#saveRDS(data_syn,"Recursos/Día2/Sesion3/0Recursos/data_syn.rds")
tba(data_syn %>% slice(1:10) %>%
      select(dam2:hat_var,theta_pred:Cv_theta_pred))

dam2	nd	pobreza	vardir	hat_var	theta_pred	thetaSyn	thetaFH	theta_pred_EE	Cv_theta_pred
00202	NA	NA	NA	NA	0.2939	0.2939	0.2939	0.0934	0.3177
00203	NA	NA	NA	NA	0.2816	0.2816	0.2816	0.0881	0.3131
00204	NA	NA	NA	NA	0.2930	0.2930	0.2930	0.0916	0.3128
00205	NA	NA	NA	NA	0.1812	0.1812	0.1812	0.0977	0.5392
00207	NA	NA	NA	NA	0.3500	0.3500	0.3500	0.0921	0.2632
00208	NA	NA	NA	NA	0.2330	0.2330	0.2330	0.1001	0.4294
00209	NA	NA	NA	NA	0.2275	0.2275	0.2275	0.1214	0.5338
00210	NA	NA	NA	NA	0.2784	0.2784	0.2784	0.1013	0.3639
00305	NA	NA	NA	NA	0.4831	0.4831	0.4831	0.0975	0.2019
00404	NA	NA	NA	NA	0.4305	0.4305	0.4305	0.1088	0.2527

consolidando las bases de estimaciones para dominios observados y NO observados.

estimacionesPre <- bind_rows(data_dir, data_syn) %>% 
  select(dam2, theta_pred)