5.3 Modelos uniparamétricos
Los modelos que están definidos en términos de un solo parámetro que pertenece al conjunto de los números reales se definen como modelos uniparamétricos.
5.3.1 Modelo de unidad: Bernoulli
Suponga que \(Y\) es una variable aleatoria con distribución Bernoulli dada por:
\[ p(Y \mid \theta)=\theta^y(1-\theta)^{1-y}I_{\{0,1\}}(y) \]
Como el parámetro \(\theta\) está restringido al espacio \(\Theta=[0,1]\), entonces es posible formular varias opciones para la distribución previa del parámetro. En particular, la distribución uniforme restringida al intervalo \([0,1]\) o la distribución Beta parecen ser buenas opciones. Puesto que la distribución uniforme es un caso particular de la distribución Beta. Por lo tanto la distribución previa del parámetro \(\theta\) estará dada por
\[ \begin{equation} p(\theta \mid \alpha,\beta)= \frac{1}{Beta(\alpha,\beta)}\theta^{\alpha-1}(1-\theta)^{\beta-1}I_{[0,1]}(\theta). \end{equation} \]
y la distribución posterior del parámetro \(\theta\) sigue una distribución
\[ \begin{equation*} \theta \mid Y \sim Beta(y+\alpha,\beta-y+1) \end{equation*} \]
Cuando se tiene una muestra aleatoria \(Y_1,\ldots,Y_n\) de variables con distribución Bernoulli de parámetro \(\theta\), entonces la distribución posterior del parámetro de interés es
\[ \begin{equation*} \theta \mid Y_1,\ldots,Y_n \sim Beta\left(\sum_{i=1}^ny_i+\alpha,\beta-\sum_{i=1}^ny_i+n\right) \end{equation*} \]
Obejtivo
Estimar la proporción de personas que están por debajo de la linea pobreza. Es decir, \[ P = \frac{\sum_{U}y_i}{N} \] donde \(y_i\) toma el valor de 1 cuando el ingreso de la persona es menor a la linea de pobreza 0 en caso contrario
El estimador de \(P\) esta dado por:
\[ \hat{P} = \frac{\sum_{s}w_{i}y_{i}}{\sum_{s}{w_{i} }} \]
con \(w_i\) el factor de expansión para la \(i-ésima\) observación. Además, y obtener \(\widehat{Var}\left(\hat{P}\right)\).
5.3.1.1 Práctica en R
library(tidyverse)
encuesta <- readRDS("Recursos/Día2/Sesion1/Data/encuestaDOM21N1.rds") Sea \(Y\) la variable aleatoria
\[ Y_{i}=\begin{cases} 1 & ingreso<lp\\ 0 & ingreso\geq lp \end{cases} \]
El tamaño de la muestra es de 6796 en la dam 1
datay <- encuesta %>% filter(dam_ee == 1) %>%
transmute(y = ifelse(ingcorte < lp, 1,0))
addmargins(table(datay$y))| 0 | 1 | Sum |
|---|---|---|
| 5063 | 1733 | 6796 |
Un grupo de estadístico experto decide utilizar una distribución previa Beta, definiendo los parámetros de la distribución previa como \(Beta(\alpha=1, \beta=1)\). La distribución posterior del parámetro de interés, que representa la probabilidad de estar por debajo de la linea de pobreza, es \(Beta(1733 + 1, 1 - 1733 + 6796)=Beta(1734, 5064)\)
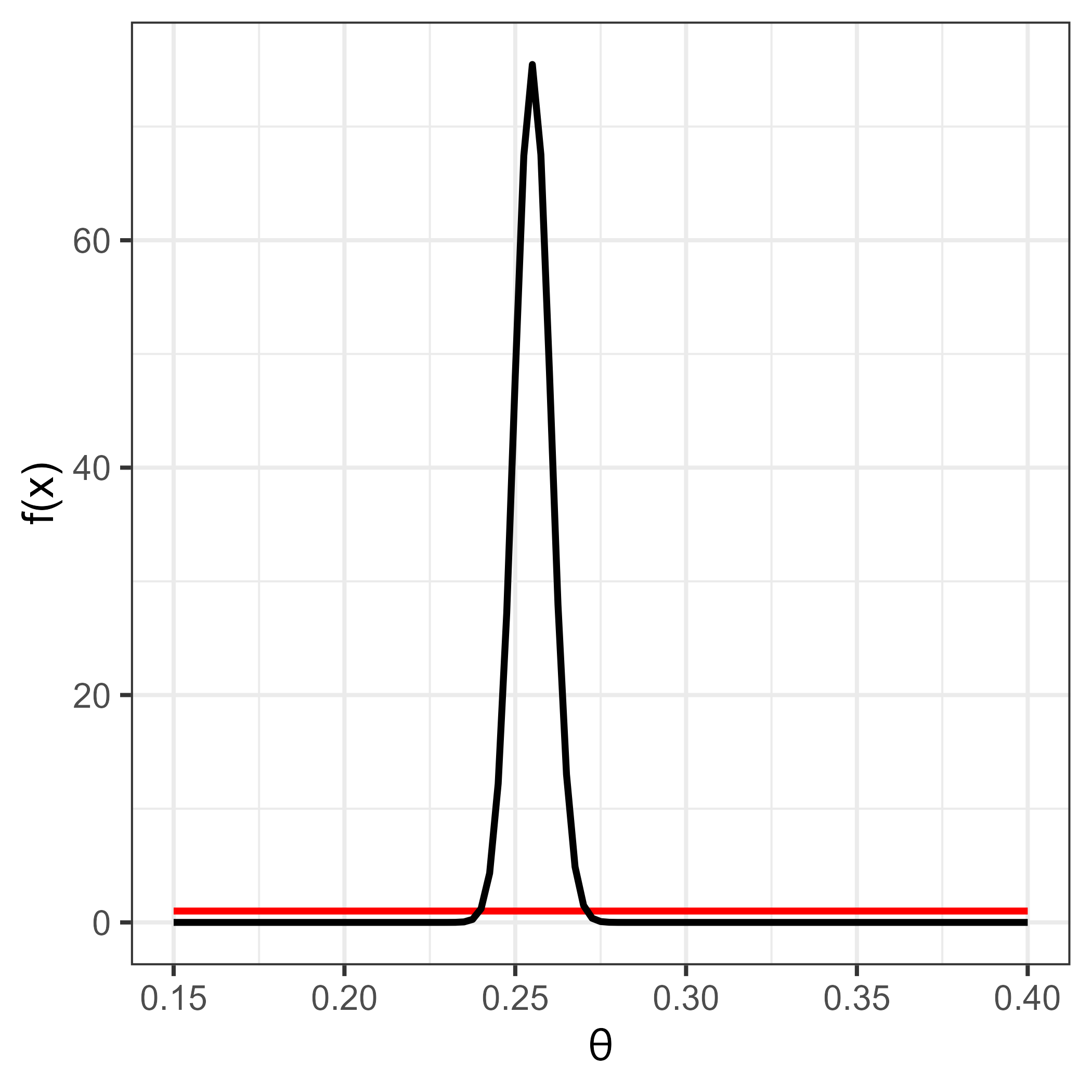
Figura 5.1: Distribución previa (línea roja) y distribución posterior (línea negra)
La estimación del parámetro estaría dado por:
\[ E(X) = \frac{\alpha}{\alpha + \beta} = \frac{1734}{1734+ 5064} = 0.255075 \]
luego, el intervalo de credibilidad para la distribución posterior es.
n = length(datay$y)
n1 = sum(datay$y)
qbeta(c(0.025, 0.975),
shape1 = 1 + n1,
shape2 = 1 - n1 + n)## [1] 0.2447824 0.26550415.3.1.2 Práctica en STAN
En STAN es posible obtener el mismo tipo de inferencia creando cuatro cadenas cuya distribución de probabilidad coincide con la distribución posterior del ejemplo.
data { // Entrada el modelo
int<lower=0> n; // Numero de observaciones
int y[n]; // Vector de longitud n
real a;
real b;
}
parameters { // Definir parámetro
real<lower=0, upper=1> theta;
}
model { // Definir modelo
y ~ bernoulli(theta);
theta ~ beta(a, b); // Distribución previa
}
generated quantities {
real ypred[n]; // vector de longitud n
for (ii in 1:n){
ypred[ii] = bernoulli_rng(theta);
}
}Para compilar STAN debemos definir los parámetros de entrada
sample_data <- list(n = nrow(datay),
y = datay$y,
a = 1,
b = 1)Para ejecutar STAN en R tenemos la librería rstan
library(rstan)
Bernoulli <- "Recursos/Día2/Sesion1/Data/modelosStan/1Bernoulli.stan"options(mc.cores = parallel::detectCores())
rstan::rstan_options(auto_write = TRUE) # speed up running time
model_Bernoulli <- stan(
file = Bernoulli, # Stan program
data = sample_data, # named list of data
verbose = FALSE,
warmup = 500, # number of warmup iterations per chain
iter = 1000, # total number of iterations per chain
cores = 4, # number of cores (could use one per chain)
)
saveRDS(model_Bernoulli,
file = "Recursos/Día2/Sesion1/0Recursos/Bernoulli/model_Bernoulli.rds")
model_Bernoulli <- readRDS("Recursos/Día2/Sesion1/0Recursos/Bernoulli/model_Bernoulli.rds")La estimación del parámetro \(\theta\) es:
tabla_Ber1 <- summary(model_Bernoulli, pars = "theta")$summary
tabla_Ber1 %>% tba()| mean | se_mean | sd | 2.5% | 25% | 50% | 75% | 97.5% | n_eff | Rhat | |
|---|---|---|---|---|---|---|---|---|---|---|
| theta | 0.255 | 2e-04 | 0.0053 | 0.2445 | 0.2515 | 0.255 | 0.2584 | 0.2657 | 703.8891 | 1.0011 |
Para observar las cadenas compilamos las lineas de código
library(posterior)
library(ggplot2)
temp <- as_draws_df(as.array(model_Bernoulli,pars = "theta"))
p1 <- ggplot(data = temp, aes(x = theta))+
geom_density(color = "blue", size = 2) +
stat_function(fun = posterior1,
args = list(y = datay$y),
size = 2) +
theme_bw(base_size = 20) +
labs(x = latex2exp::TeX("\\theta"),
y = latex2exp::TeX("f(\\theta)"))
#ggsave(filename = "Recursos/Día2/Sesion1/0Recursos/Bernoulli/Bernoulli2.png",plot = p1)
p1 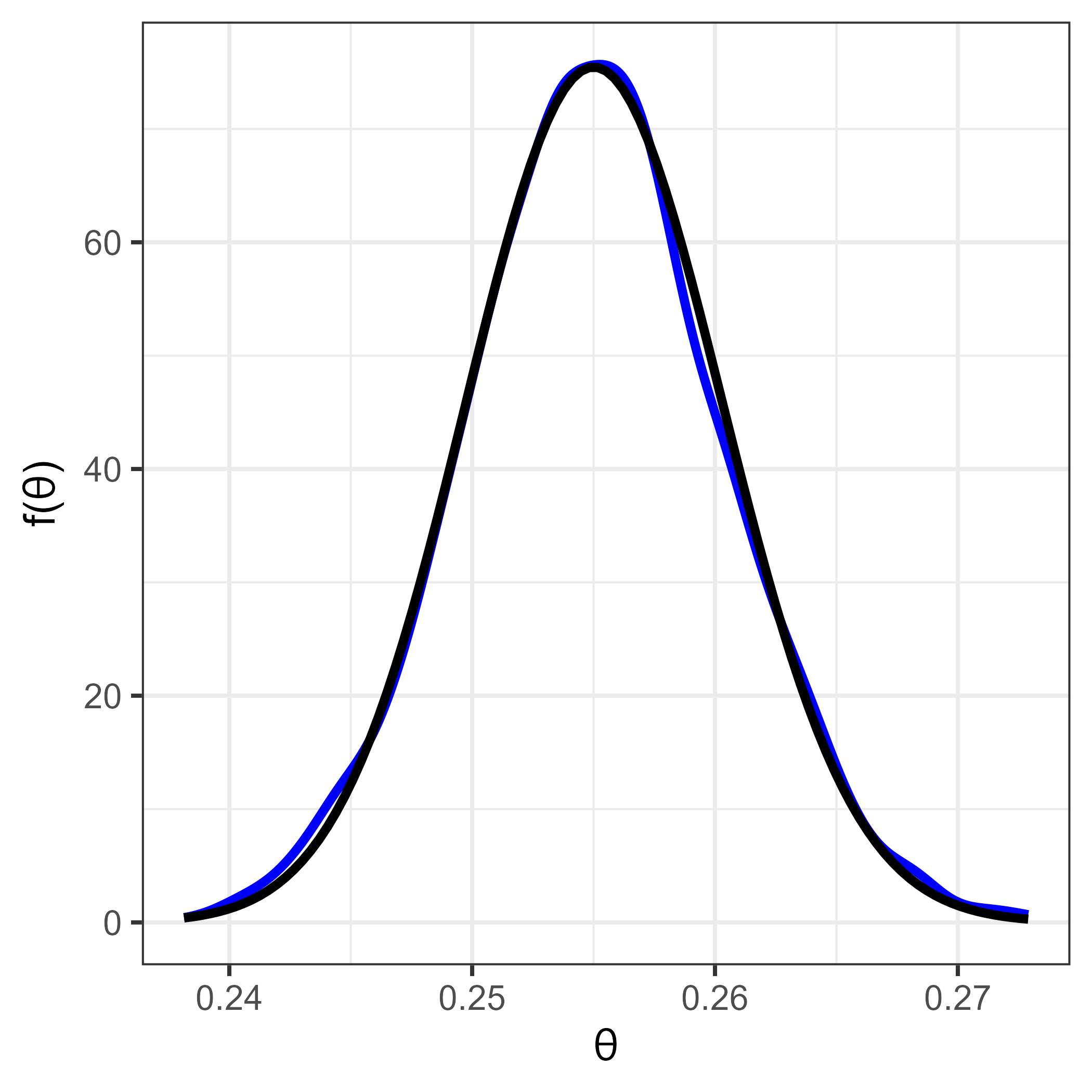
Figura 5.2: Resultado con STAN (línea azul) y posterior teórica (línea negra)
Para validar las cadenas
library(bayesplot)
library(patchwork)
posterior_theta <- as.array(model_Bernoulli, pars = "theta")
(mcmc_dens_chains(posterior_theta) +
mcmc_areas(posterior_theta) ) /
traceplot(model_Bernoulli, pars = "theta", inc_warmup = T)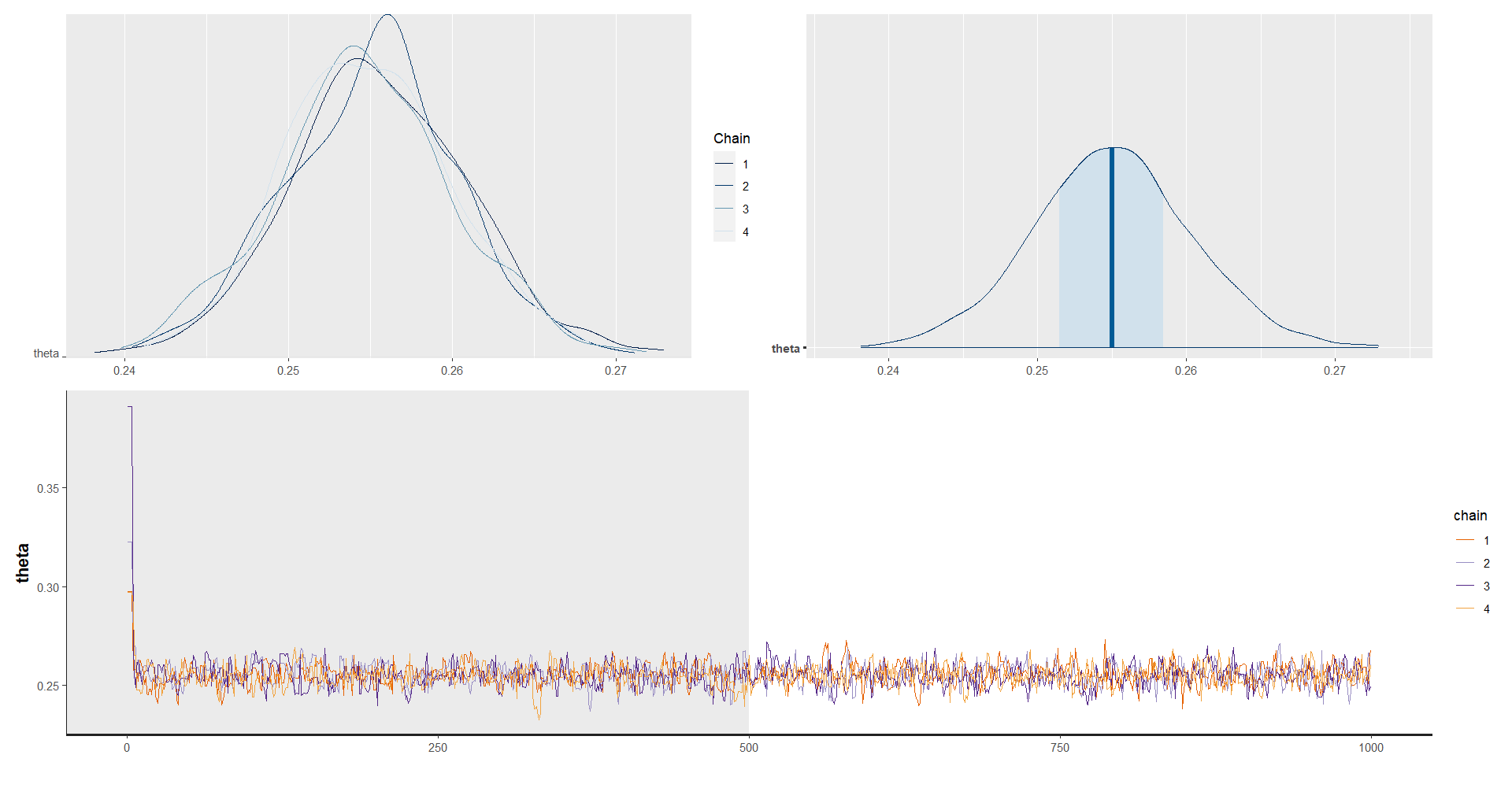
Predicción de \(Y\) en cada una de las iteraciones de las cadenas.
y_pred_B <- as.array(model_Bernoulli, pars = "ypred") %>%
as_draws_matrix()
rowsrandom <- sample(nrow(y_pred_B), 100)
y_pred2 <- y_pred_B[rowsrandom, 1:n]
ppc_dens_overlay(y = datay$y, y_pred2)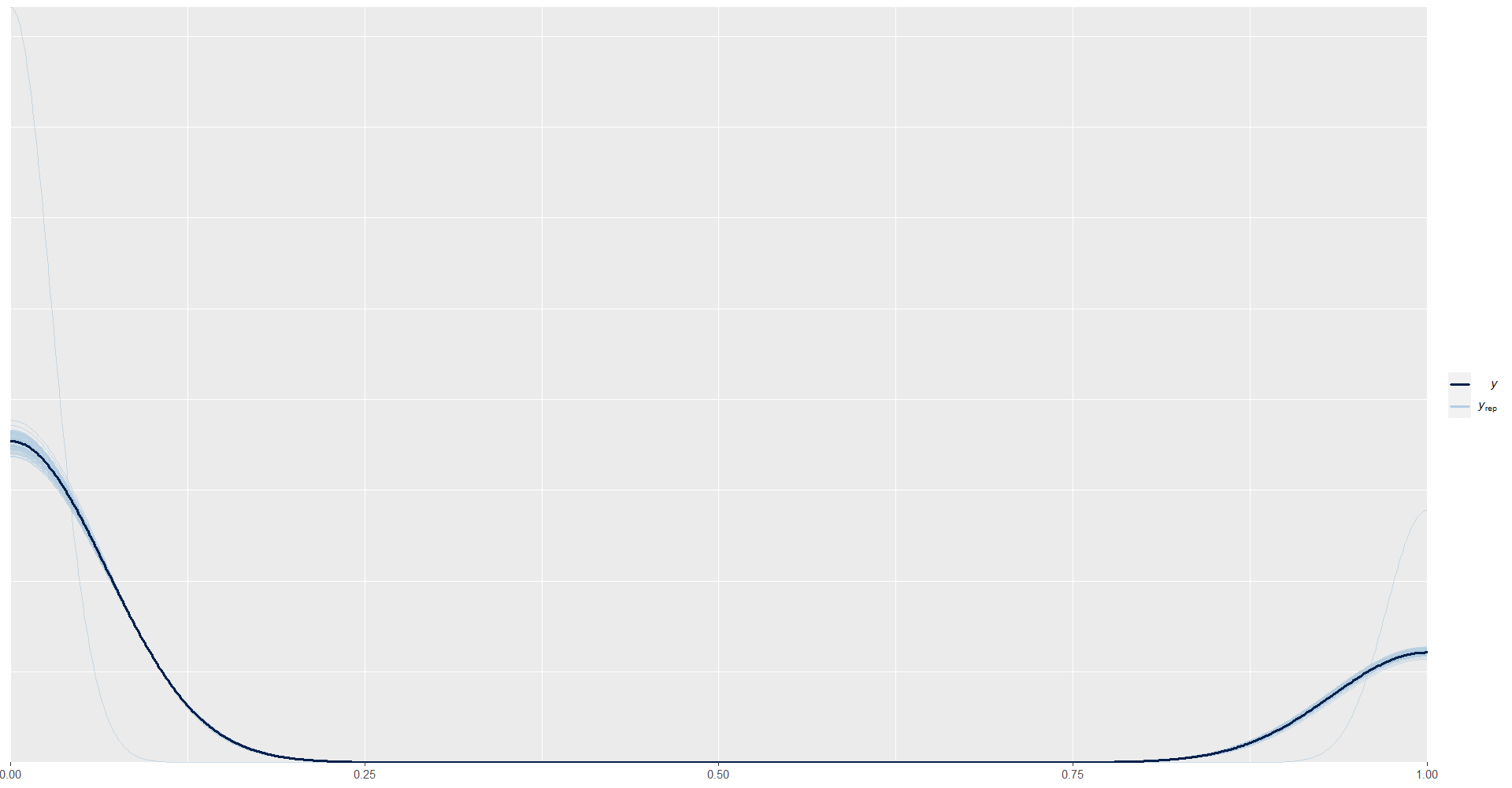
5.3.2 Modelo de área: Binomial
Cuando se dispone de una muestra aleatoria de variables con distribución Bernoulli \(Y_1,\ldots,Y_n\), la inferencia Bayesiana se puede llevar a cabo usando la distribución Binomial, puesto que es bien sabido que la suma de variables aleatorias Bernoulli
\[ \begin{equation*} S=\sum_{i=1}^nY_i \end{equation*} \]
sigue una distribución Binomial. Es decir:
\[ \begin{equation} p(S \mid \theta)=\binom{n}{s}\theta^s(1-\theta)^{n-s}I_{\{0,1,\ldots,n\}}(s), \end{equation} \]
Nótese que la distribución Binomial es un caso general para la distribución Bernoulli, cuando \(n=1\). Por lo tanto es natural suponer que distribución previa del parámetro \(\theta\) estará dada por
\[ \begin{equation} p(\theta \mid \alpha,\beta)= \frac{1}{Beta(\alpha,\beta)}\theta^{\alpha-1}(1-\theta)^{\beta-1}I_{[0,1]}(\theta). \end{equation} \]
La distribución posterior del parámetro \(\theta\) sigue una distribución
\[ \begin{equation*} \theta \mid S \sim Beta(s+\alpha,\beta-s+n) \end{equation*} \]
Ahora, cuando se tiene una sucesión de variables aleatorias \(S_1,\ldots,S_d, \ldots,S_D\) independientes y con distribución \(Binomial(n_d,\theta_d)\) para \(d=1,\ldots,K\), entonces la distribución posterior del parámetro de interés \(\theta_d\) es
\[ \begin{equation*} \theta_d \mid s_d \sim Beta\left(s_d+\alpha,\ \beta+ n_d- s_d\right) \end{equation*} \]
Obejtivo
Estimar la proporción de personas que están por debajo de la linea pobreza en el \(d-ésimo\) dominio. Es decir,
\[ P_d = \frac{\sum_{U_d}y_{di}}{N_d} \] donde \(y_i\) toma el valor de 1 cuando el ingreso de la persona es menor a la linea de pobreza 0 en caso contrario.
El estimador de \(P\) esta dado por:
\[ \hat{P_d} = \frac{\sum_{s_d}w_{di}y_{di}}{\sum_{s_d}{w_{di} }} \]
con \(w_{di}\) el factor de expansión para la \(i-ésima\) observación en el \(d-ésimo\) dominio.
5.3.2.1 Práctica en STAN
Sea \(S_k\) el conteo de personas en condición de pobreza en el \(k-ésimo\) departamento en la muestra.
dataS <- encuesta %>%
transmute(
dam = dam_ee,
y = ifelse(ingcorte < lp, 1,0)
) %>% group_by(dam) %>%
summarise(nd = n(), #Número de ensayos
Sd = sum(y) #Número de éxito
)
tba(dataS)| dam | nd | Sd |
|---|---|---|
| 1 | 6796 | 1733 |
| 2 | 1556 | 397 |
| 3 | 2013 | 979 |
| 4 | 2912 | 1093 |
| 5 | 466 | 125 |
| 6 | 1649 | 295 |
| 7 | 821 | 365 |
| 8 | 1199 | 268 |
| 9 | 2012 | 235 |
| 10 | 1200 | 561 |
| 11 | 2678 | 432 |
| 12 | 2543 | 744 |
| 13 | 2534 | 416 |
| 14 | 780 | 195 |
| 15 | 773 | 96 |
| 16 | 466 | 203 |
| 17 | 1059 | 214 |
| 18 | 2907 | 381 |
| 19 | 460 | 9 |
| 20 | 669 | 162 |
| 21 | 3381 | 1012 |
| 22 | 2318 | 625 |
| 23 | 2260 | 368 |
| 24 | 909 | 138 |
| 25 | 9011 | 1840 |
| 26 | 401 | 55 |
| 27 | 963 | 171 |
| 28 | 923 | 157 |
| 29 | 1619 | 675 |
| 30 | 478 | 84 |
| 31 | 346 | 80 |
| 32 | 17969 | 4554 |
Creando código de STAN
data {
int<lower=0> K; // Número de provincia
int<lower=0> n[K]; // Número de ensayos
int<lower=0> s[K]; // Número de éxitos
real a;
real b;
}
parameters {
real<lower=0, upper=1> theta[K]; // theta_d|s_d
}
model {
for(kk in 1:K) {
s[kk] ~ binomial(n[kk], theta[kk]);
}
to_vector(theta) ~ beta(a, b);
}
generated quantities {
real spred[K]; // vector de longitud K
for(kk in 1:K){
spred[kk] = binomial_rng(n[kk],theta[kk]);
}
}Preparando el código de STAN
Binomial2 <- "Recursos/Día2/Sesion1/Data/modelosStan/3Binomial.stan"Organizando datos para STAN
sample_data <- list(K = nrow(dataS),
s = dataS$Sd,
n = dataS$nd,
a = 1,
b = 1)Para ejecutar STAN en R tenemos la librería rstan
options(mc.cores = parallel::detectCores())
model_Binomial2 <- stan(
file = Binomial2, # Stan program
data = sample_data, # named list of data
verbose = FALSE,
warmup = 500, # number of warmup iterations per chain
iter = 1000, # total number of iterations per chain
cores = 4, # number of cores (could use one per chain)
)
saveRDS(model_Binomial2, "Recursos/Día2/Sesion1/0Recursos/Binomial/model_Binomial2.rds")
model_Binomial2 <- readRDS("Recursos/Día2/Sesion1/0Recursos/Binomial/model_Binomial2.rds")La estimación del parámetro \(\theta\) es:
tabla_Bin1 <-summary(model_Binomial2, pars = "theta")$summary
tabla_Bin1 %>% tba()| mean | se_mean | sd | 2.5% | 25% | 50% | 75% | 97.5% | n_eff | Rhat | |
|---|---|---|---|---|---|---|---|---|---|---|
| theta[1] | 0.2550 | 1e-04 | 0.0054 | 0.2443 | 0.2514 | 0.2549 | 0.2586 | 0.2663 | 5541.426 | 0.9984 |
| theta[2] | 0.2557 | 2e-04 | 0.0111 | 0.2346 | 0.2480 | 0.2555 | 0.2633 | 0.2775 | 4685.553 | 0.9988 |
| theta[3] | 0.4863 | 2e-04 | 0.0112 | 0.4639 | 0.4790 | 0.4863 | 0.4937 | 0.5081 | 4275.709 | 0.9995 |
| theta[4] | 0.3754 | 1e-04 | 0.0090 | 0.3578 | 0.3692 | 0.3756 | 0.3815 | 0.3930 | 4356.266 | 0.9993 |
| theta[5] | 0.2688 | 3e-04 | 0.0210 | 0.2310 | 0.2543 | 0.2682 | 0.2831 | 0.3099 | 5505.855 | 0.9987 |
| theta[6] | 0.1792 | 1e-04 | 0.0095 | 0.1612 | 0.1729 | 0.1790 | 0.1858 | 0.1983 | 5539.281 | 0.9985 |
| theta[7] | 0.4447 | 3e-04 | 0.0172 | 0.4108 | 0.4336 | 0.4445 | 0.4562 | 0.4795 | 4289.643 | 0.9989 |
| theta[8] | 0.2240 | 2e-04 | 0.0115 | 0.2019 | 0.2161 | 0.2238 | 0.2315 | 0.2470 | 4261.208 | 0.9993 |
| theta[9] | 0.1172 | 1e-04 | 0.0077 | 0.1023 | 0.1121 | 0.1170 | 0.1222 | 0.1328 | 3835.345 | 0.9994 |
| theta[10] | 0.4673 | 2e-04 | 0.0142 | 0.4402 | 0.4577 | 0.4671 | 0.4769 | 0.4949 | 5121.700 | 0.9992 |
| theta[11] | 0.1617 | 1e-04 | 0.0071 | 0.1483 | 0.1568 | 0.1614 | 0.1667 | 0.1760 | 5501.146 | 0.9983 |
| theta[12] | 0.2930 | 1e-04 | 0.0089 | 0.2759 | 0.2870 | 0.2928 | 0.2988 | 0.3105 | 4834.824 | 0.9987 |
| theta[13] | 0.1644 | 1e-04 | 0.0073 | 0.1503 | 0.1595 | 0.1643 | 0.1691 | 0.1788 | 5452.961 | 0.9981 |
| theta[14] | 0.2505 | 2e-04 | 0.0148 | 0.2216 | 0.2404 | 0.2505 | 0.2598 | 0.2813 | 3949.950 | 0.9985 |
| theta[15] | 0.1253 | 2e-04 | 0.0120 | 0.1024 | 0.1170 | 0.1250 | 0.1334 | 0.1484 | 3561.371 | 0.9985 |
| theta[16] | 0.4359 | 3e-04 | 0.0228 | 0.3920 | 0.4206 | 0.4356 | 0.4507 | 0.4811 | 4413.229 | 0.9989 |
| theta[17] | 0.2030 | 2e-04 | 0.0122 | 0.1803 | 0.1949 | 0.2024 | 0.2106 | 0.2285 | 3553.277 | 0.9984 |
| theta[18] | 0.1313 | 1e-04 | 0.0061 | 0.1193 | 0.1272 | 0.1313 | 0.1355 | 0.1428 | 3265.019 | 0.9987 |
| theta[19] | 0.0217 | 1e-04 | 0.0068 | 0.0105 | 0.0168 | 0.0211 | 0.0258 | 0.0367 | 4589.526 | 0.9989 |
| theta[20] | 0.2427 | 3e-04 | 0.0163 | 0.2119 | 0.2310 | 0.2426 | 0.2539 | 0.2754 | 3692.533 | 0.9985 |
| theta[21] | 0.2995 | 1e-04 | 0.0081 | 0.2833 | 0.2941 | 0.2995 | 0.3047 | 0.3152 | 4654.262 | 0.9994 |
| theta[22] | 0.2701 | 1e-04 | 0.0091 | 0.2520 | 0.2642 | 0.2701 | 0.2759 | 0.2884 | 4987.638 | 0.9986 |
| theta[23] | 0.1630 | 1e-04 | 0.0080 | 0.1477 | 0.1573 | 0.1628 | 0.1684 | 0.1788 | 3848.725 | 0.9985 |
| theta[24] | 0.1524 | 2e-04 | 0.0114 | 0.1310 | 0.1442 | 0.1522 | 0.1603 | 0.1752 | 3602.961 | 0.9989 |
| theta[25] | 0.2042 | 1e-04 | 0.0041 | 0.1964 | 0.2014 | 0.2041 | 0.2070 | 0.2122 | 4184.041 | 0.9995 |
| theta[26] | 0.1388 | 3e-04 | 0.0177 | 0.1069 | 0.1265 | 0.1381 | 0.1505 | 0.1760 | 4957.831 | 0.9985 |
| theta[27] | 0.1783 | 2e-04 | 0.0118 | 0.1560 | 0.1700 | 0.1783 | 0.1863 | 0.2028 | 4550.942 | 0.9987 |
| theta[28] | 0.1706 | 2e-04 | 0.0125 | 0.1467 | 0.1618 | 0.1705 | 0.1796 | 0.1950 | 4629.408 | 0.9993 |
| theta[29] | 0.4171 | 2e-04 | 0.0126 | 0.3926 | 0.4084 | 0.4168 | 0.4257 | 0.4418 | 5023.648 | 0.9989 |
| theta[30] | 0.1772 | 3e-04 | 0.0176 | 0.1442 | 0.1651 | 0.1764 | 0.1884 | 0.2137 | 4571.020 | 0.9988 |
| theta[31] | 0.2328 | 4e-04 | 0.0227 | 0.1895 | 0.2177 | 0.2324 | 0.2477 | 0.2811 | 4051.155 | 0.9993 |
| theta[32] | 0.2535 | 1e-04 | 0.0032 | 0.2473 | 0.2514 | 0.2535 | 0.2557 | 0.2597 | 3530.149 | 0.9992 |
Para validar las cadenas
(s1 <- mcmc_areas(as.array(model_Binomial2, pars = "theta")))
# ggsave(filename = "Recursos/Día2/Sesion1/0Recursos/Binomial/Binomial1.png",plot = s1)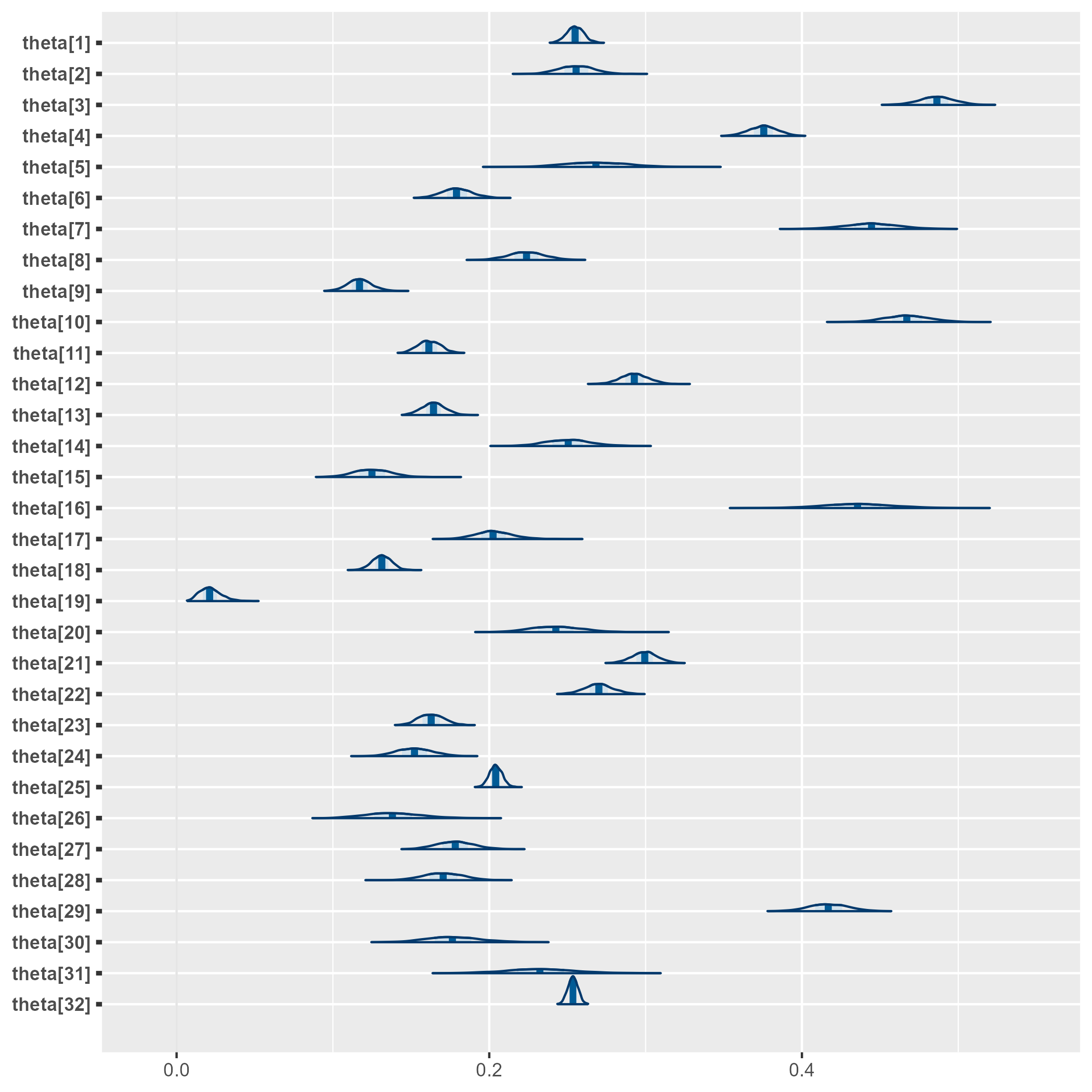
(s2 <- mcmc_trace(as.array(model_Binomial2, pars = "theta")))
# ggsave(filename = "Recursos/Día2/Sesion1/0Recursos/Binomial/Binomial2.png",
# plot = s2,width = 20, height = 20, units = "cm")
y_pred_B <- as.array(model_Binomial2, pars = "spred") %>%
as_draws_matrix()
rowsrandom <- sample(nrow(y_pred_B), 200)
y_pred2 <- y_pred_B[rowsrandom, ]
g1 <- ggplot(data = dataS, aes(x = Sd))+
geom_histogram(aes(y = ..density..)) +
geom_density(size = 2, color = "blue") +
labs(y = "")+
theme_bw(10) +
yaxis_title(FALSE) + xaxis_title(FALSE) + yaxis_text(FALSE) +
yaxis_ticks(FALSE)
g2 <- ppc_dens_overlay(y = dataS$Sd, y_pred2)
g1/g2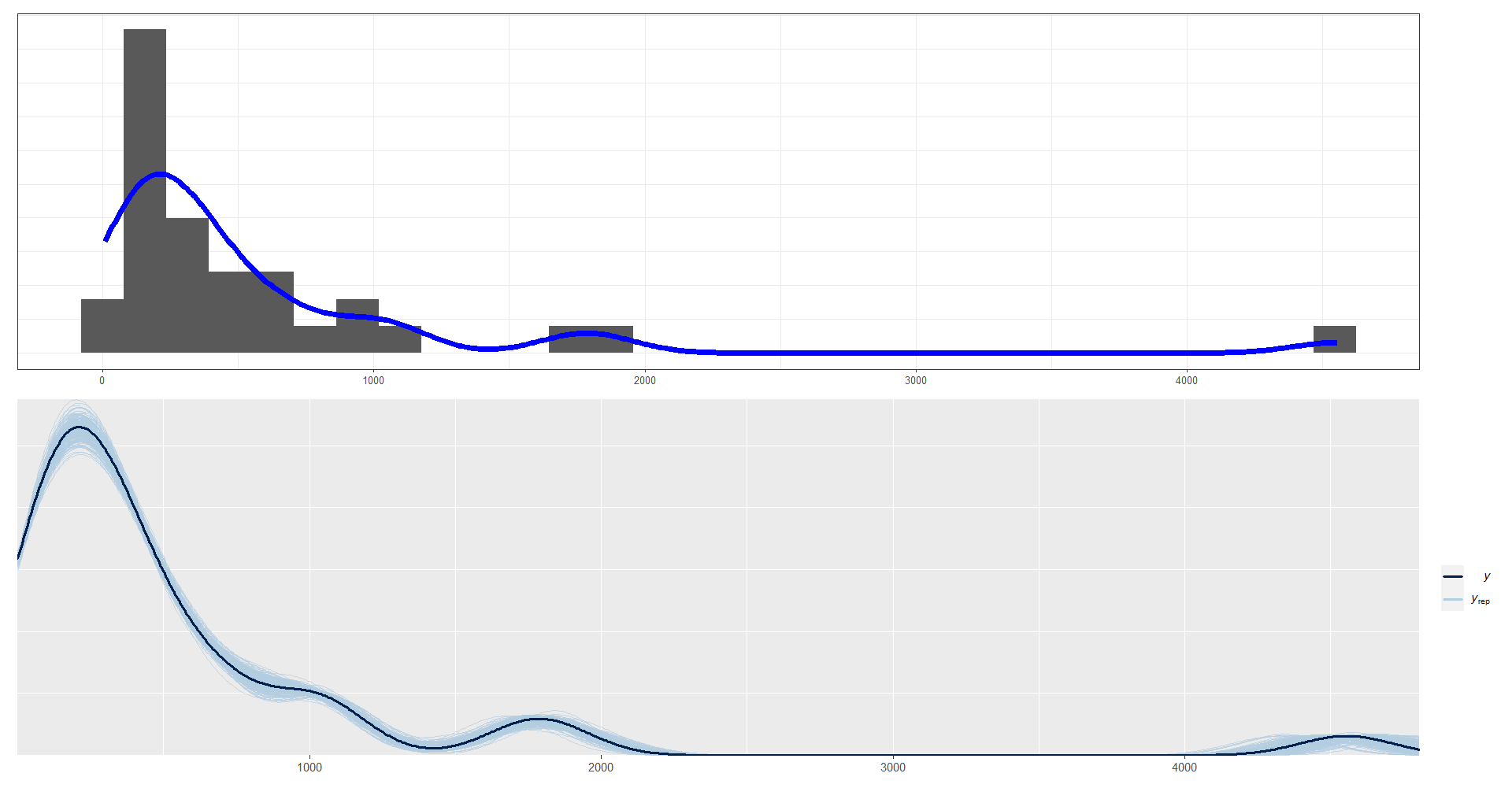
5.3.3 Modelo de unidad: Normal con media desconocida
Suponga que \(Y_1,\cdots,Y_n\) son variables independientes e idénticamente distribuidos con distribución \(Normal(\theta,\sigma^2)\) con \(\theta\) desconocido pero \(\sigma^2\) conocido. De esta forma, la función de verosimilitud de los datos está dada por
\[ \begin{align*} p(\mathbf{Y} \mid \theta) &=\prod_{i=1}^n\frac{1}{\sqrt{2\pi\sigma^2}}\exp\left\{-\frac{1}{2\sigma^2}(y_i-\theta)^2\right\}I_\mathbb{R}(y) \\ &=(2\pi\sigma^2)^{-n/2}\exp\left\{-\frac{1}{2\sigma^2}\sum_{i=1}^n(y_i-\theta)^2\right\} \end{align*} \]
Como el parámetro \(\theta\) puede tomar cualquier valor en los reales, es posible asignarle una distribución previa \(\theta \sim Normal(\mu,\tau^2)\). Bajo este marco de referencia se tienen los siguientes resultados
La distribución posterior del parámetro de interés \(\theta\) sigue una distribución
\[ \begin{equation*} \theta|\mathbf{Y} \sim Normal(\mu_n,\tau^2_n) \end{equation*} \]
En donde
\[ \begin{equation} \mu_n=\frac{\frac{n}{\sigma^2}\bar{Y}+\frac{1}{\tau^2}\mu}{\frac{n}{\sigma^2}+\frac{1}{\tau^2}} \ \ \ \ \ \ \ \text{y} \ \ \ \ \ \ \ \tau_n^2=\left(\frac{n}{\sigma^2}+\frac{1}{\tau^2}\right)^{-1} \end{equation} \]
Obejtivo
Estimar el ingreso medio de la población, es decir,
\[ \bar{Y} = \frac{\sum_Uy_i}{N} \] donde, \(y_i\) es el ingreso de las personas. El estimador de \(\bar{Y}\) esta dado por \[ \hat{\bar{Y}} = \frac{\sum_{s}w_{i}y_{i}}{\sum_s{w_i}} \] y obtener \(\widehat{Var}\left(\hat{\bar{Y}}\right)\).
5.3.3.1 Práctica en STAN
Sea \(Y\) el logaritmo del ingreso
dataNormal <- encuesta %>%
transmute(
dam_ee ,
logIngreso = log(ingcorte +1)) %>%
filter(dam_ee == 1)
#3
media <- mean(dataNormal$logIngreso)
Sd <- sd(dataNormal$logIngreso)
g1 <- ggplot(dataNormal,aes(x = logIngreso))+
geom_density(size = 2, color = "blue") +
stat_function(fun =dnorm,
args = list(mean = media, sd = Sd),
size =2) +
theme_bw(base_size = 20) +
labs(y = "", x = ("Log(Ingreso)"))
g2 <- ggplot(dataNormal, aes(sample = logIngreso)) +
stat_qq() + stat_qq_line() +
theme_bw(base_size = 20)
g1|g2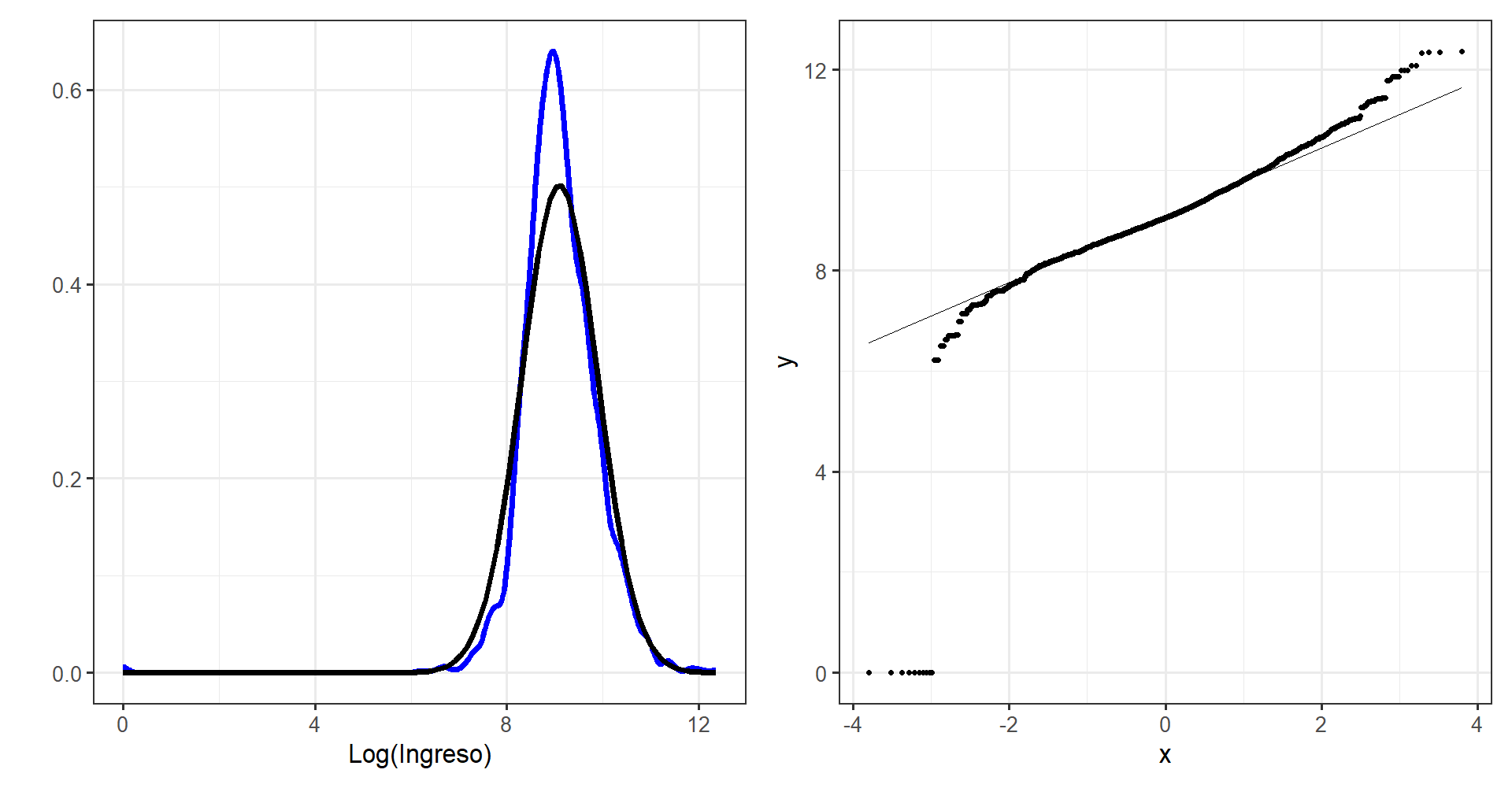
Creando código de STAN
data {
int<lower=0> n; // Número de observaciones
real y[n]; // LogIngreso
real <lower=0> Sigma; // Desviación estándar
}
parameters {
real theta;
}
model {
y ~ normal(theta, Sigma);
theta ~ normal(0, 1000); // Distribución previa
}
generated quantities {
real ypred[n]; // Vector de longitud n
for(kk in 1:n){
ypred[kk] = normal_rng(theta,Sigma);
}
}Preparando el código de STAN
NormalMedia <- "Recursos/Día2/Sesion1/Data/modelosStan/4NormalMedia.stan" Organizando datos para STAN
sample_data <- list(n = nrow(dataNormal),
Sigma = sd(dataNormal$logIngreso),
y = dataNormal$logIngreso)Para ejecutar STAN en R tenemos la librería rstan
options(mc.cores = parallel::detectCores())
model_NormalMedia <- stan(
file = NormalMedia,
data = sample_data,
verbose = FALSE,
warmup = 500,
iter = 1000,
cores = 4
)
saveRDS(model_NormalMedia, "Recursos/Día2/Sesion1/0Recursos/Normal/model_NormalMedia.rds")
model_NormalMedia <-
readRDS("Recursos/Día2/Sesion1/0Recursos/Normal/model_NormalMedia.rds")La estimación del parámetro \(\theta\) es:
tabla_Nor1 <- summary(model_NormalMedia, pars = "theta")$summary
tabla_Nor1 %>% tba() | mean | se_mean | sd | 2.5% | 25% | 50% | 75% | 97.5% | n_eff | Rhat | |
|---|---|---|---|---|---|---|---|---|---|---|
| theta | 9.0982 | 4e-04 | 0.0095 | 9.0786 | 9.0917 | 9.0985 | 9.1046 | 9.1167 | 654.8346 | 1.0008 |
posterior_theta <- as.array(model_NormalMedia, pars = "theta")
(mcmc_dens_chains(posterior_theta) +
mcmc_areas(posterior_theta) ) /
mcmc_trace(posterior_theta)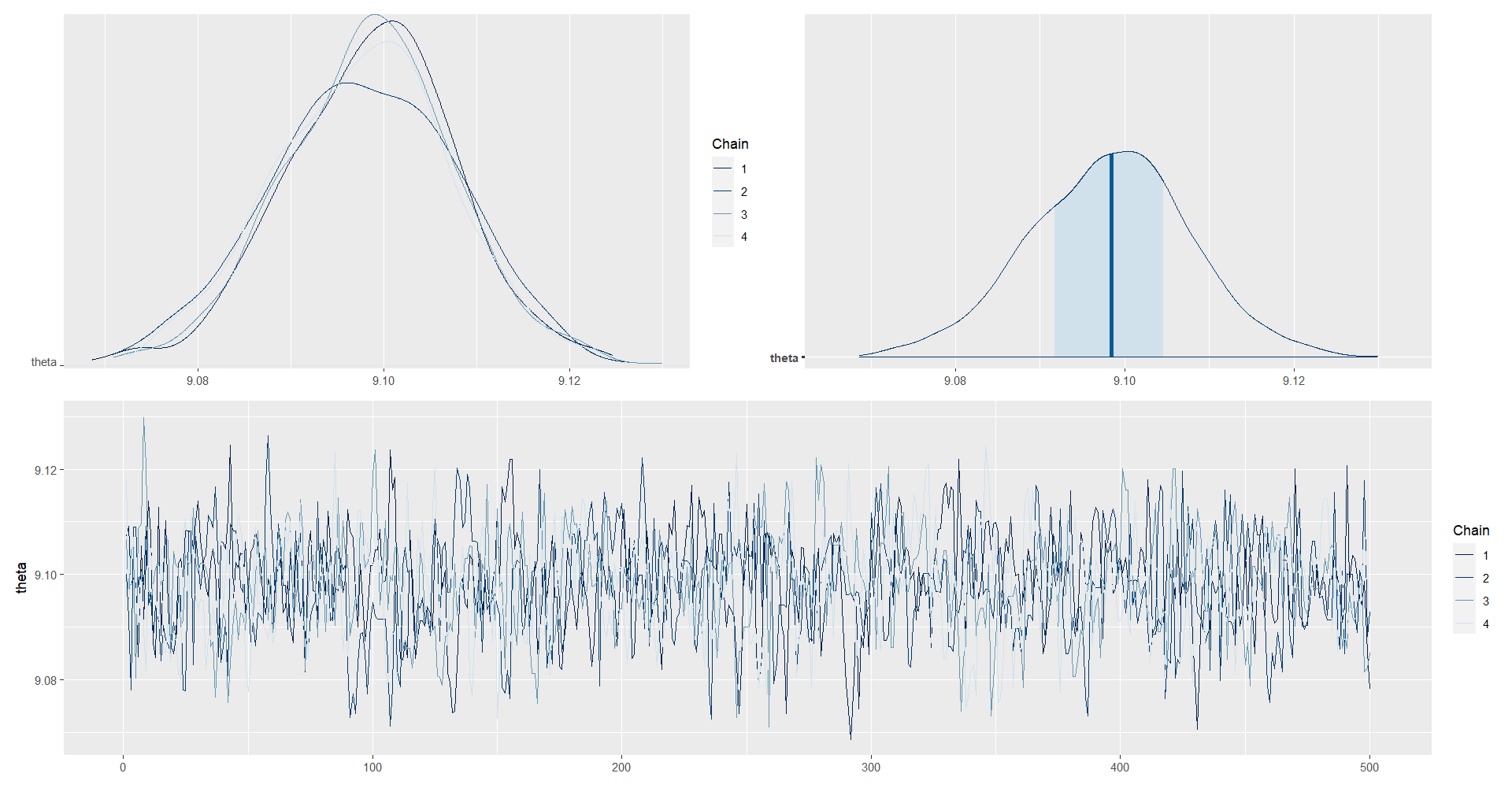
y_pred_B <- as.array(model_NormalMedia, pars = "ypred") %>%
as_draws_matrix()
rowsrandom <- sample(nrow(y_pred_B), 100)
y_pred2 <- y_pred_B[rowsrandom, ]
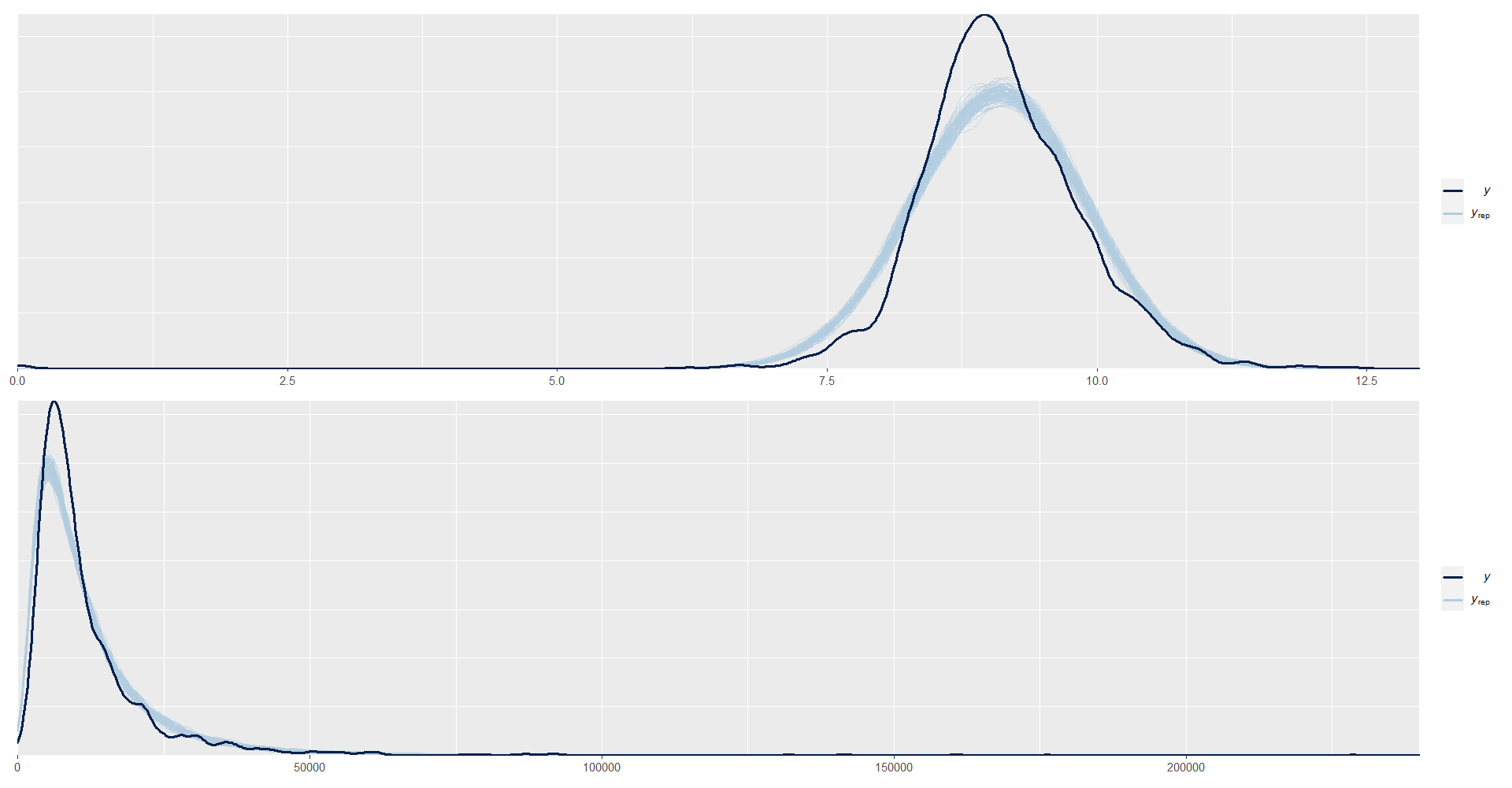
ppc_dens_overlay(y = as.numeric(dataNormal$logIngreso), y_pred2)/
ppc_dens_overlay(y = exp(as.numeric(dataNormal$logIngreso))-1, exp(y_pred2)-1) + xlim(0,240000)