14.3 Consideraciones sobre la imputación múltiple
Antes de escoger un método particular, es pertinente observar qué efectos conlleva esta escogencia en las propiedades estadísticas de los estimadores en las encuestas de hogares. En cuanto a la imputación múltiple, las propiedades estadísticas de los estimadores deben ser modificadas acordemente. Subestimar la variación de las estimaciones puede ser un error muy grave, puesto que afecta la cobertura nominal de los intervalos de confianza y a su vez influye en las pruebas de hipótesis y en el cálculo de los valores \(p\).
Por ejemplo, suponga que existe una muestra aleatoria \(s\) compuesta por un conjunto de \(n\) datos que relacionan dos variables \(X\), \(Y\), a través del siguiente modelo de regresión simple:
\[ y_k = \beta x_k + \varepsilon_k \]
En donde los errores tienen distribución normal con \(E(\varepsilon_k) = 0\) y \(Var(\varepsilon_k) = \sigma ^2\) para todo \(k\in s\). Bajo esta perspectiva, suponga que la variable dependiente de interés sólo pudo ser observada para un conjunto de individuos de tamaño \(n_1\), mientras que para los \(n_0\) individuos restantes (es decir, \(n_1 + n_0 = n\)), no existen datos para la variable de interés; además se asume que sí fue posible observar los valores de la covariable \(X\) para todos los individuos en la muestra.
El valor agregado de la imputación múltiple (Rubin 1987) realmente está en la estimación de los errores estándar. No tener en cuenta la naturaleza estocástica de los valores imputados arroja estimaciones de la varianza mucho menores. La idea consiste en generar \(M > 1\) conjuntos de valores para los registros faltantes. Al final, el valor imputado corresponderá al promedio de esos \(M\) valores. Por tanto el modelo final de imputación (para los valores faltantes) toma la siguiente forma:
\[\dot{y}_i = \dot{\beta} x_{i_{(missing)}}+ \dot{\varepsilon_i}\]
Para este caso, se consideran dos maneras de realizar la imputación; la primera basada en la esperanza del modelo (sin imputación múltiple) y la segunda basada en la adición del término de error del modelo (imputación múltiple):
- Ingenua: en este escenario, el valor imputado para el registro faltante toma la siguiente forma: \[ \dot{y}_i = \hat\beta x_{i_{(missing)}} \] Esta clase de imputación carece de aleatoriedad y por tanto, la varianza de \(\beta\) será subestimada.
- Múltiple: en este caso, se tiene en cuenta el término de error en la generación de los valores imputados, tales que \[ \dot{y}_i = \dot{\beta} x_{i_{(missing)}}+ \dot{\varepsilon_i} \]
Es posible realizar la imputación múltiple de forma frecuentista o bayesiana. Por ejemplo, es posible seleccionar \(M\) muestras bootstrap, y para cada una se estiman los parámetros \(\beta\) y \(\sigma\) para generar \(\dot{y}_i\). Al final se promedian los \(M\) valores y se imputa el valor faltante. Por otro lado, teniendo en cuenta el acercamiento bayesiano, se definen las distribuciones posteriores de \(\beta\) y \(\sigma\) para generar \(M\) valores de estos parámetros y por tanto \(M\) valores de \(\dot{y}_i\). De igual manera, al final se promedian los \(M\) valores y se imputa el valor faltante.
Por ejemplo, si el interés es la estimación de un parámetro \(\beta\), entonces la esperanza estimada al utilizar la metodología de imputación múltiple está dada por:
\[ E(\hat{\beta} | Y_{obs}) = E(E(\hat{\beta} | Y_{obs}, Y_{mis}) | Y_{obs}) \]
Esta expresión es estimada por el promedio de las \(M\) estimaciones puntuales de \(\hat{\beta}\) sobre las \(M\) imputaciones, dado por:
\[ \bar{\hat{\beta}} = \frac{1}{M} \sum_{m = 1} ^ M \hat{\beta}_m \]
Entre tanto, la varianza estimada al utilizar la metodología de imputación múltiple está dada por la siguiente expresión:
\[ V(\hat{\beta} | Y_{obs}) = E(V(\hat{\beta} | Y_{obs}, Y_{mis}) | Y_{obs}) + V(E(\hat{\beta} | Y_{obs}, Y_{mis}) | Y_{obs}) \]
La primera parte de la anterior expresión se estima como el promedio de las varianzas muestrales de \(\hat{\beta}\) sobre las \(M\) imputaciones, dado por:
\[ \bar{U} = \frac{1}{M} \sum_{m = 1} ^ M Var(\hat{\beta}) \]
El segundo término se estima como la varianza muestral de las \(M\) estimaciones puntuales de \(\hat{\beta}\) sobre las \(M\) imputaciones, dada por: \[ B = \frac{1}{M-1} \sum_{m = 1} ^ M (\hat{\beta}_m - \bar{\hat{\beta}})^2 \]
Además, es necesario tener en cuenta un factor de corrección (puesto que \(M\) es finito). Por tanto, la estimación del segundo término viene dada por la siguiente expresión:
\[ \left(1 + \frac{1}{M}\right) B \]
Por tanto, la varianza estimada es igual a:
\[ \hat{V}(\hat{\beta} | Y_{obs}) = \bar{U} + \left(1 + \frac{1}{M}\right) B \]
Por ejemplo, si se quiere realizar mediciones de pobreza utilizando la imputación múltiple es necesario primero establecer un modelo sobre los ingresos \(y_k\) y luego generar \(Q\) posibles valores \(y_k^q \ (q=1, \ldots, Q)\) para cada individuo que no respondió. Luego, utilizando los \(Q\) conjuntos de datos completos, es necesario estimar la siguientes cantidades
\[ \hat{F}_{\alpha}^{q}=\frac{1}{N}\sum_{k\in s} w_k \left(\frac{l-y_k}{l}\right)^{\alpha}I(y_k<l) \ \ \ \ \ \ \ \ \ q= 1,\ldots, Q. \]
El estimador final basado en la técnica de imputación múltiple será el promedio simple de las anteriores estimaciones, dado por
\[ \tilde{F}_{\alpha}=\frac{1}{Q}\sum_{q=1}^Q \hat{F}_{\alpha}^{q} \]
La varianza de esta metodología se puede dividir en dos componentes, el primero correspondiente a la variación dentro de cada conjunto de datos creado, y el segundo correspondiente a la variación entre cada estimación resultante. Por lo tanto, la varianza asociada a \(\tilde{F}_{\alpha}\) es
\[ \hat{V}(\tilde{F}_{\alpha}) = \frac{1}{Q}\sum_{q=1}^Q \hat{V}(\hat{F}_{\alpha}^{q}) + \left(1+\frac{1}{Q}\right)\frac{1}{Q-1}\sum_{q=1}^Q (\hat{F}_{\alpha}^{q}-\tilde{F}_{\alpha})^2 \]
Una vez que se tienen los conjuntos de datos completos, es posible estimar \(\hat{V}(\hat{F}_{\alpha}^{q})\) utilizando las técnicas del último conglomerado en conjunción con el Jackkinfe. La característica principal del proceso imputación es utilizar la información auxiliar para aproximar con precisión los valores faltantes. De esta forma, las estimaciones poblacionales de los parámetros de interés tendrán sesgo nulo o despreciable y la confiabilidad de la estrategia de muestreo se mantendrá como se planeó en una primera instancia. L siguiente simulación ejemplifica las ventajas de la imputación múltiple.
14.3.1 Simulación empírica
Para ejemplificar los anteriores escenarios, en esta sección se muestran los resultados empíricos de una simulación que asumió un conjunto de \(n = 100\) datos con una pendiente \(\beta = 100\) y con una dispersión de \(\sigma = 2\). A su vez, el conjunto de datos tendrá \(n_0 = 40\) valores faltantes en la variable respuesta. A continuación se muestran las primeras diez filas de esta base de datos simulados. Nótese que las dos primeras columnas corresponden a los valores verdaderos de la covariable y la variable de interés, respectivamente. La tercera columna identifica cuáles de estos valores son faltantes y la cuarta columna representaría la información disponible en la base de datos de la muestra \(s\).
| x | y | faltantes | y (no imputado) |
|---|---|---|---|
| 11 | 991 | Si | NA |
| 12 | 1282 | Si | NA |
| 12 | 1164 | No | 1164 |
| 12 | 1217 | No | 1217 |
| 13 | 1325 | No | 1325 |
| 11 | 1086 | No | 1086 |
| 12 | 1210 | Si | NA |
| 13 | 1272 | Si | NA |
| 15 | 1459 | Si | NA |
| 11 | 1182 | No | 1182 |
Con el 40% de valores faltantes, es necesario realizar una imputación para obtener registros completos en la base de datos. Para este ejemplo, la figura 14.5 relaciona las variables con (izquierda) y sin (derecha) valores faltantes se presentan a continuación.
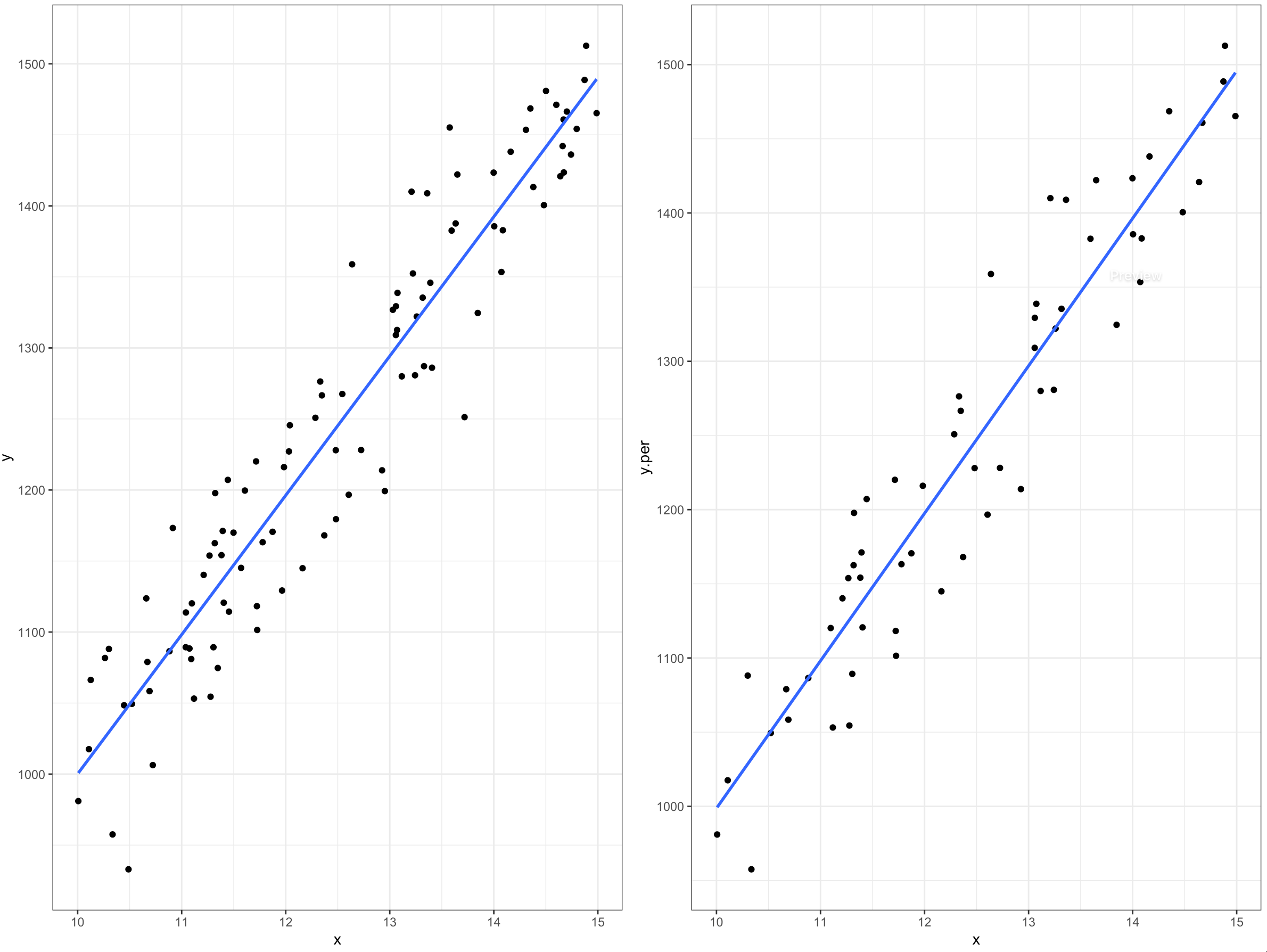
Figura 14.5: Relación de la variable de interés para los datos completos (izquierda) y con ausencia de valores (derecha).
Al aplicar una imputación ingenua, por ejemplo basada en un modelo de regresión simple, se obtendría un conjunto de datos completo, ejemplificado (solo las primeras diez filas de la base) en la siguiente tabla:
| x | y (original) | faltantes | y (imputado) |
|---|---|---|---|
| 11 | 991 | Si | 1047 |
| 12 | 1282 | Si | 1221 |
| 12 | 1164 | No | 1164 |
| 12 | 1217 | No | 1217 |
| 13 | 1325 | No | 1325 |
| 11 | 1086 | No | 1086 |
| 12 | 1210 | Si | 1221 |
| 13 | 1272 | Si | 1290 |
| 15 | 1459 | Si | 1485 |
| 11 | 1182 | No | 1182 |
En general, usar un enfoque simple no afecta la estimación puntual del parámetro de interés, sino la estimación del error estándar, puesto que la variación natural de los datos se subestima dramáticamente. Por ejemplo, la figura 14.6 muestra que con la imputación simple, todos los valores faltantes imputados están sobre la línea de regresión.
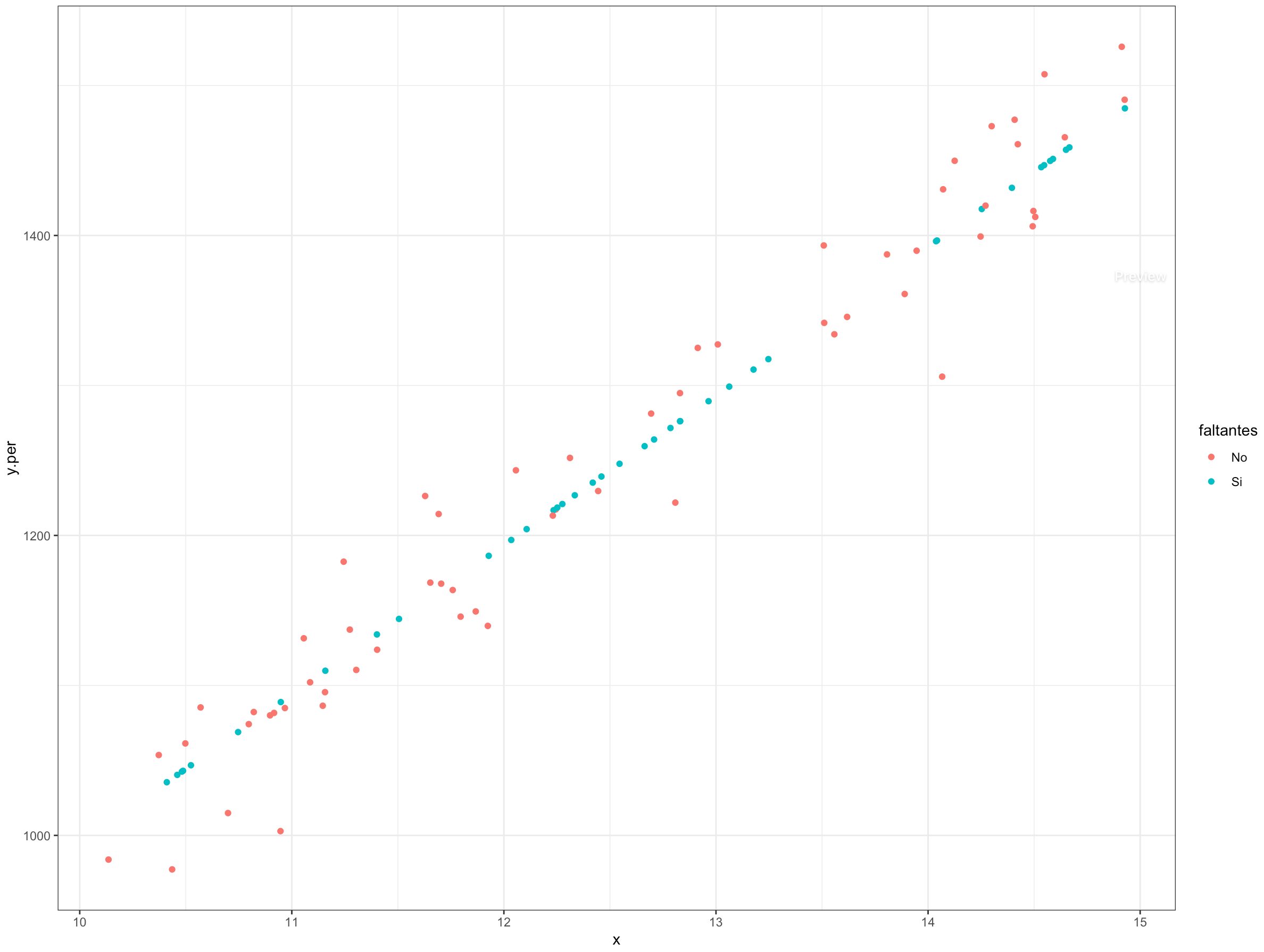
Figura 14.6: Relación de la variable de interés con la covariable auxiliar para el enfoque de imputación ingenua.
Si se considera la imputación múltiple con el enfoque bootstrap, también se obtedrá un conjunto de datos aumentado por cada una de las \(M\) realizaciones que se ejecuten. Por ejemplo, a continuación se ilustra el conjunto de datos obtenido con \(M=3\) realizaciones. Nótese que los valores de la variable de interés cambian en cada realización; estas realizaciones se conocen en la literatura como valores plausibles.
| x | y (original) | faltantes | y1 (imputado) | y2 (imputado) | y3 (imputado) |
|---|---|---|---|---|---|
| 11 | 991 | Si | 1047 | 950 | 1040 |
| 12 | 1282 | Si | 1221 | 1254 | 1198 |
| 12 | 1164 | No | 1164 | 1164 | 1164 |
| 12 | 1217 | No | 1217 | 1217 | 1217 |
| 13 | 1325 | No | 1325 | 1325 | 1325 |
| 11 | 1086 | No | 1086 | 1086 | 1086 |
| 12 | 1210 | Si | 1252 | 1199 | 1198 |
| 13 | 1272 | Si | 1304 | 1302 | 1292 |
| 15 | 1459 | Si | 1485 | 1493 | 1478 |
| 11 | 1182 | No | 1182 | 1182 | 1182 |
Existe una buena dispersión en los valores imputados y la gráfica 14.7 muestra cómo este enfoque es mucho más realista al considerar la variación natural del fenómeno de interés en los valores imputados.
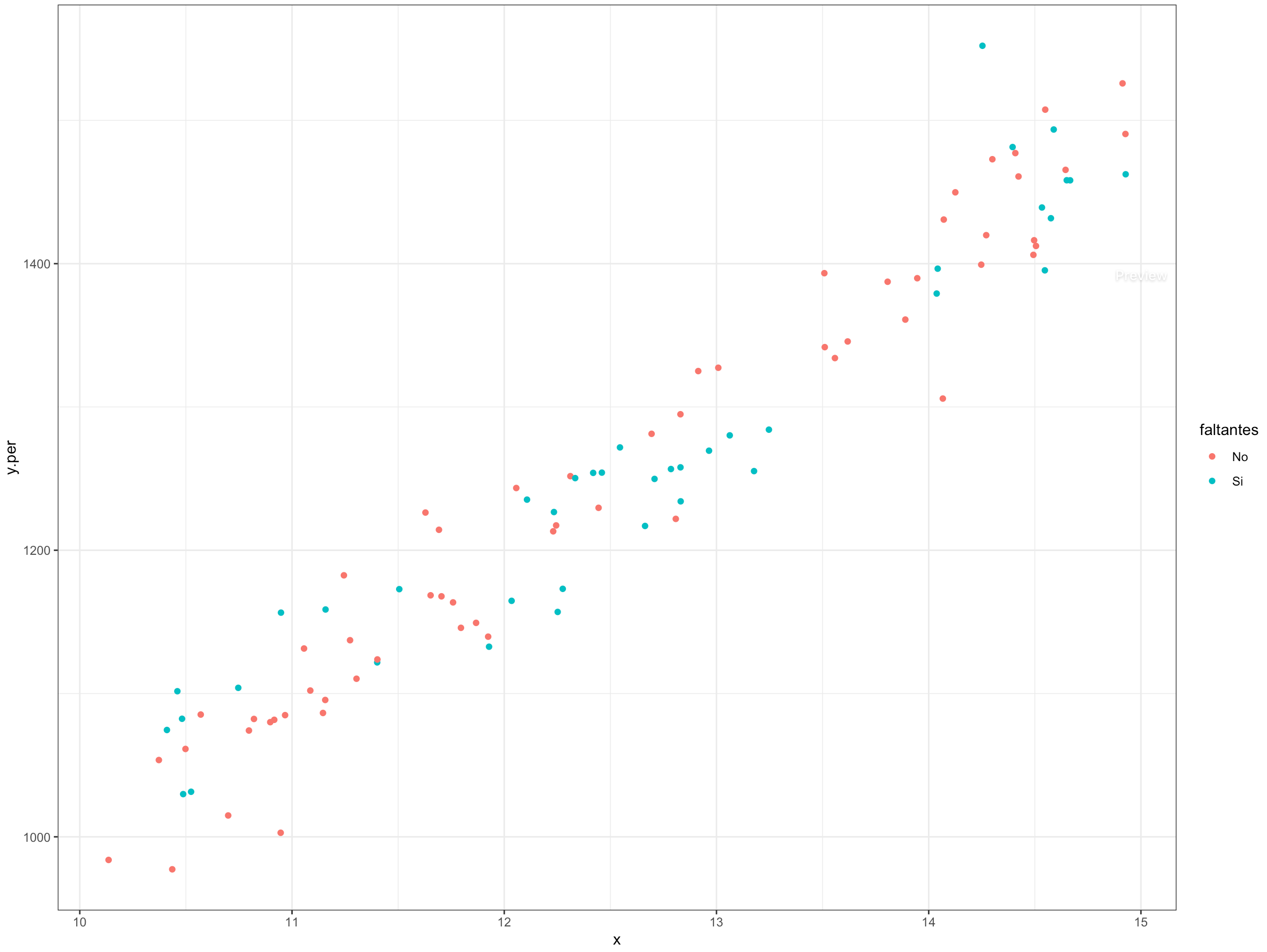
Figura 14.7: Relación de la variable de interés con la covariable auxiliar para el enfoque de imputación múltiple Bootstrap
Por otro lado, bajo distribuciones previas no informativas, es bien sabido que la distribución posterior de \(\sigma^2\) es:
\[ \sigma^2| y, x \sim \frac{\sum_{i = 1}^{n_1} (y_i - \hat{\beta} x_i)^2}{\chi ^2_{n_1-1}} \]
con \(\hat{\beta} = \frac{\sum_{i = 1}^{n_1} x_i y_i}{\sum_{i = 1}^{n_1} x_i^2}\). Asimismo, la distribución posterior de \(\beta\) es:
\[ \beta | \sigma^2, y, x \sim Normal \left(\hat{\beta}, \frac{\sigma^2}{\sum_{i = 1}^{n_1} x_i^2} \right) \]
Asumiendo el anterior enfoque bayesiano de imputación múltiple, se llega a resultados similares. En ambos casos existe una buena dispersión en los valores imputados, respetando la distribución natural de la característica de interés. La siguiente gráfica así lo demuestra.
En resumen, a partir de esta simulación de Monte Carlo, se concluye rápidamente que imputar de manera determinista puede conllevar a la subestimación de la dispersión de la variable de interés. La siguiente tabla muestra que los tres métodos de imputación arrojaron estimaciones puntuales insesgadas. Sin embargo, el error estándar de la estimación simple es gravemente subestimado. De esta forma, la amplitud de los intervalos de confianza al 95% inducidos por la estimación simple es inferior al de los otros dos métodos, causando que la cobertura del método simple sea deficiente, pues su nivel nominal en realidad no es del 95%, sino del 83%.
| Propiedades | Ingenuo | Bootstrap | Bayesiano |
|---|---|---|---|
| Esperanza | 100.00 | 100.01 | 100.01 |
| Error estándar | 0.24 | 0.41 | 0.42 |
| Amplitud | 0.96 | 1.60 | 1.66 |
| Cobertura | 0.83 | 0.97 | 0.95 |