11.5 Función generalizada de varianzas
Existe también la posibilidad de estimar las varianzas de los estimadores de muestreo (definido sobre la medida de probabilidad inducida por el diseño de muestreo \(p\)) mediante un modelo (definido sobre una medida de probabilidad \(m\)) que simplifica el proceso computacional en la generación de las miles de estimaciones que se producen a partir de las encuestas de hogares en la región. Wolter (2007) afirma que si los parámetros de este modelo pueden ser estimados a partir de encuestas pasadas o de un conjunto de datos reducido, entonces las estimaciones de la varianza (y por consiguiente las estimaciones del error de muestreo) pueden se producidas simplemente evaluando el modelo a los datos actuales de la encuesta.
Un caso particular de este tipo de relaciones se presenta cuando se deben obtener estimaciones de la encuesta a nivel subnacional para la publicación de cuadros de salida conteniendo la estimación puntual y el error estándar estimado. En estos casos es muy común que la cantidad total de celdas en los cuadros de salida sea muy grande, por lo que una mejor opción, en términos de eficiencia computacional, puede ser la utilización de este tipo de modelos, denominados en la literatura como GVF (Generalized Variance Function). Otro caso especial que debe ser atendido por el personal técnico de las ONE es cuando el tamaño de muestra de las subpoblaciones de interés es pequeño, o cuando no hay la suficiente heterogeneidad entre las observaciones de la muestra en la subpoblación. En este caso, es muy probable que las estimaciones de la varianza de los estimadores de los totales, tamaños, proporciones o medias sean imprecisas. En efecto, no es poco común encontrar estimaciones de la varianza iguales a cero. En este caso, este tipo de estimaciones deben ser cotejadas con experticia y/o reemplazadas por una mejor aproximación, que puede estar sustentada en las GVF.
Un aspecto importante en la modelación de las varianzas de los estimadores es reconocer la naturaleza de este parámetro, el cual será siempre positivo. Por ende, al tratar de modelarlas es útil tomar un acercamiento log-lineal, que permite lidiar con este tipo de estructuras. La siguiente figura muestra la relación que puede establecerse entre las estimaciones directas de las proporciones de pobreza municipal y el logaritmo de sus varianzas estimadas.
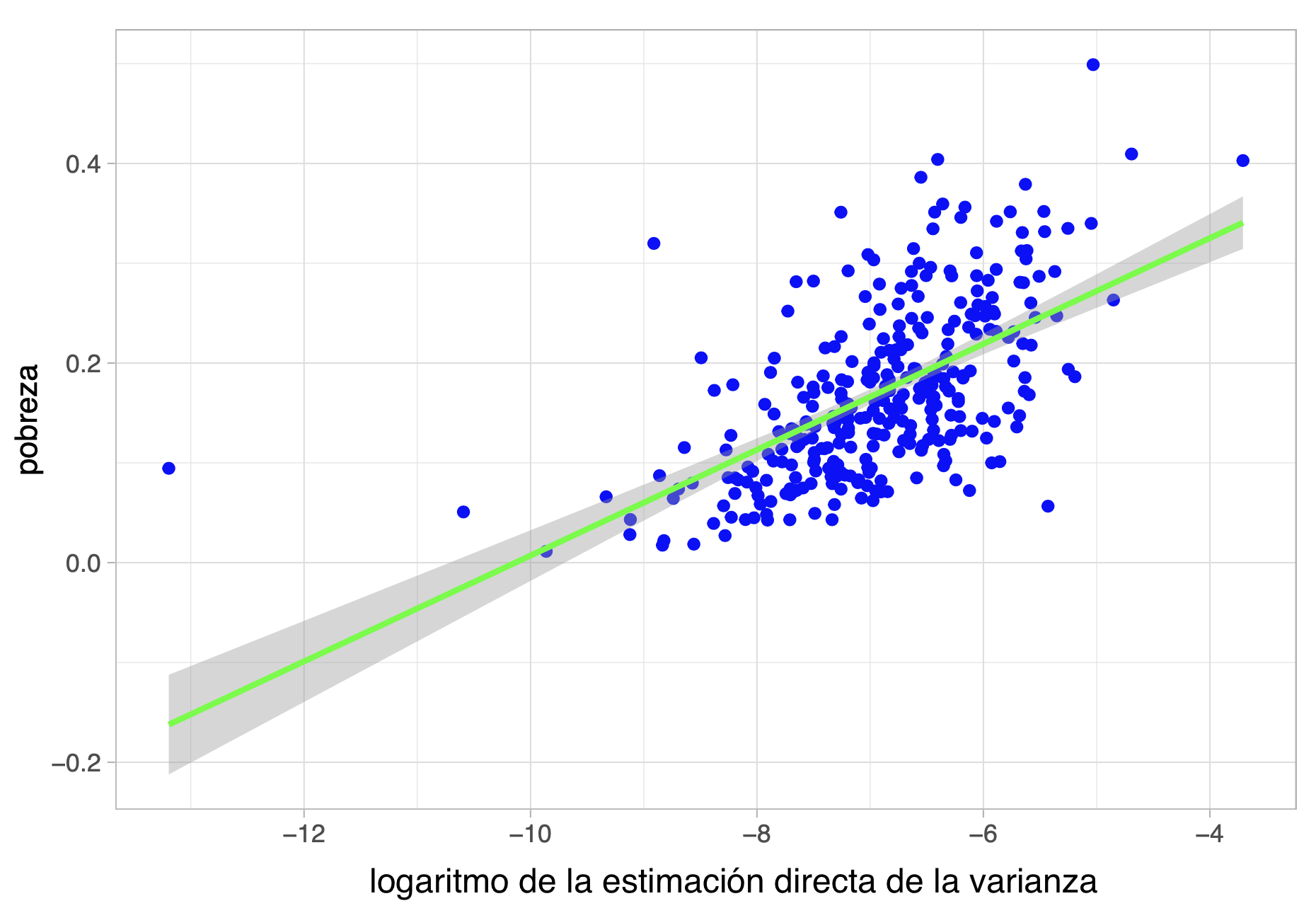
Relación entre un estimador de la tasa de pobreza estimada y el logaritmo de la estimación directa de su varianza. Fuente: elaboración propia.
En términos de notación \(Var_{GVF}(\hat{\theta}) = E_m(\widehat{Var}(\hat{\theta}))\) será la varianza suavizada del estimador directo \(\hat{\theta}\). Un aspecto importante en este tipo de modelos es que, en general, no es posible tratar a \(Var(\hat{\theta})\) como un valor fijo puesto que no es estrictamente una función de las covariables auxiliares. Partiendo del hecho de que se tiene acceso a un estimador insesgado de \({Var}(\hat{\theta})\), denotado por \(\widehat{Var}(\hat{\theta})\) se tiene que:
\[ E_{mp}\left(\widehat{Var}(\hat{\theta})\right) = E_m\left(E_p\left(\widehat{Var}(\hat{\theta})\right)\right) = E_m({Var}(\hat{\theta})) = Var_{GVF}(\hat{\theta}) \]
La anterior igualdad contiene subscritos \(m\) y \(p\) que hacen referencia a la medida de probabilidad del modelo y del diseño de muestreo, respectivamente. Nótese que aunque el diseño de muestreo induce estimadores de las varianzas que son insesgados, estos tienden a ser inestable cuando el tamaño de muestra es pequeño, que es justo el paradigma dominante en la desagregación de estimaciones. Rivest y Belmonte (2000) consideran modelos de suavizamiento para la estimación de las varianzas directas definidos de la siguiente manera:
\[ \log(\widehat{Var}(\hat{\theta})) = \mathbf z_d' \boldsymbol \alpha + \varepsilon_d \]
En donde \(\mathbf z_d\) es un vector de covariables explicativas, \(\boldsymbol \alpha\) es un vector de parámetros que deben ser estimados, \(\varepsilon_d\) son errores aleatorios con media cero y varianza constante, que se asumen idénticamente distribuidos condicionalmente sobre \(\mathbf z_d\). Del anterior modelo, la estimación suavizada de la varianza de muestreo está dada por:
\[ Var_{GVF}(\hat{\theta}) = E_{mp}(\widehat{Var}(\hat{\theta})) = \exp(\mathbf z_d' \boldsymbol \alpha) \cdot \Delta \]
En donde, \(E_{mp}(\varepsilon_d) = \Delta\). No hay necesidad de especificar una distribución paramétrica para los errores de este modelo. Al utilizar el método de los momentos, se tiene el siguiente estimador insesgado para \(\Delta\):
\[ \hat\Delta = \frac{\sum_{d=1}^D \widehat{Var}(\hat{\theta})}{\sum_{d=1}^D \exp(\mathbf z_d' \boldsymbol \alpha)} \]
De la misma forma, al utilizar mínimos cuadrados ordinarios, la estimación del coeficiente de parámetros de regresión está dada por la siguiente expresión:
\[ \hat{\boldsymbol \alpha} = \left(\sum_{d=1}^D \mathbf z_d \mathbf z_d' \right)^{-1} \sum_{d=1}^D \mathbf z_d \log(\widehat{Var}(\hat{\theta})) \]
Por último, el estimador suavizado de la varianza muestral está definido por:
\[ \widehat{Var}_{GVF}(\hat{\theta}) = \exp(\mathbf z_d'\hat{\boldsymbol \alpha})\hat\Delta \]
Rivest y Belmonte (2000) además concluyeron que este estimador no sobrestima ni subestima la varianza suavizada, puesto que el promedio de las estimaciones suavizadas \(\widehat{Var}_{GVF}(\hat{\theta})\) coincide con el promedio de las varianzas directas \(\widehat{{Var}}(\hat{\theta})\). Por tanto:
\[ \frac{\sum_{d=1}^D \widehat{Var}_{GVF}(\hat{\theta}) }{D} = \frac{\sum_{d=1}^D \widehat{{Var}}(\hat{\theta})}{D} \]
El Instituto de Estadísticas de Canadá (Statcan) utiliza este tipo de modelos para reportar cifras oficiales del mercado de trabajo para 149 áreas censales (Beaumont y Bocci 2016). En primer lugar, Statcan hace una exclusión para el ajuste del modelo de aquellas áreas con menos de 10 personas en la fuerza de trabajo (denominador del indicador). De la misma manera todas las áreas con estimador de varianza directa \(\widehat{{Var}}(\hat{\theta})\) igual a cero son excluidas del modelo, puesto que implicaría que no se encontró ningún caso efectivo en el numerador del indicador. Asimismo, la estimación de la varianza directa está basada en el diseño de muestreo complejo, mientras que la estimación de la varianza suavizada está supeditada al siguiente modelo de regresión: \[ \log(\widehat{Var}(\hat{\theta})) = \mathbf z_d' \boldsymbol \alpha + \varepsilon_d \] En donde \[ \mathbf z_d'=\left(1, \log\left(\frac{N_d^{EIB}}{N_d^{15+}}\right), \log\left(1-\frac{N_d^{EIB}}{N_d^{15+}}\right), \log\left(N_d^{15+}\right)\right)' \] Con \(N_d^{EIB}\), el número de beneficiarios del seguro de desempleo en el área \(d\) y \(N_d^{15+}\), el número de personas en la fuerza de trabajo. Para las áreas con un tamaño de casos efectivo mayor a 400, para evitar posibles sesgos en las áreas con tamaño de muestra grande, se decidió que la estimación suavizada por GVF fuese igual a la estimación directa; es decir, \(\widehat{Var}_{GVF}(\hat{\theta}) = \widehat{Var}(\hat{\theta})\).
En otra aplicación práctica, Fuquene et al. (2019) estiman la prevalencia de migrantes internacionales en los municipios de Colombia mediante un modelo de área en el cual utilizan el enfoque GVF, con un modelo que se plantea en términos de una relación log-lineal con el siguiente vector de covariables auxiliares:
\[ \mathbf z_d'=\left(1, \ \hat\theta_d, \ \sqrt{\hat\theta_d}, \ n_d, \ \sqrt{n_d}, \ \sqrt{\hat\theta_d \times n_d} \ \right)' \]
Asimismo, una de las aplicaciones más citadas se presenta en Fay y Herriot (1979). En este artículo seminal de los modelos de estimación en áreas pequeñas, se relata que el United States Census Bureau realizó un censo con una muestra co-censal del 20% en cada estado para estimar el ingreso percápita. Para estimar este indicador a nivel desagregado se utilizó la estimación directa acompañada con un GVF de varianzas como estimador suavizado. Este modelo tomó los resultados de ocho estados y generalizó para el resto del país. Como resultado de esta modelación, el coeficiente de variación y la varianza se establecieron como una función del tamaño del área.
En la región, MDSF y CEPAL (2021) utilizaron un modelo GVF para estimar las varianzas de las tasas de pobreza comunal a partir de la CASEN 2020. En este modelo la variable dependiente fue el logaritmo natural de la estimación de la varianza directa de las tasas de pobreza y como covariables se incluyeron al intercepto, a la estimación directa de la tasa de pobreza, al tamaño de muestra comunal, a la interacción entre la tasa de pobreza y el tamaño de muestra, a la raíz cuadrada de la tasa de pobreza, a la raíz cuadrada del tamaño de muestra y, por último, a la raíz cuadrada de la interacción entre la tasa de pobreza y el tamaño de muestra. Las comunas incluidas en la modelación que tuvieron una tasa nula de pobreza, y por consiguiente una estimación nula de la varianza del estimador directo no fueron incluidas en el ajuste del modelo, pero sí se obtuvieron las predicciones de sus varianzas. En el mencionado reporte se muestra esquemas descriptivos que justifican la inclusión de las covariables y las relaciones establecidas en el modelo. Además, el factor de ajuste \(\hat\Delta\) estuvo cercano a 1.2 en todas las series estudiadas.