5.5 Evaluación y escogencia de la mejor estratificación
En la evaluación de los escenarios de estratificación entran las técnicas univariadas y multivariadas. Al final, el resultado de aplicar una u otra técnica es simplemente una clasificación de las UPM. Por lo tanto, cada una de las posibles estratificaciones debe ser evaluada con base en la reducción de la varianza para todos los indicadores considerados en la matriz de clasificación. La medida clásica con la que se juzgan las bondades de una estrategia de muestreo es el efecto de diseño (DEFF). Por lo tanto, la evaluación de la estratificación debe estar supeditada también a esta medida, que para la variable \(p = 1, \ldots, P\), está dada por:
\[ DEFF_p = \frac{Var_{ST}(\bar x _p)}{Var_{SI}(\bar x _p)} \ \ \ \ \ \ \ \ \ p = 1, \ldots, P. \]
En donde, \(Var_{ST}(\bar x _p)\) y \(Var_{SI}(\bar x _p)\) denotan la varianza del diseño estratificado y la varianza de un muestreo aleatorio simple para la media poblacional (porcentaje) de la \(p\)-ésima variable de la matriz de información. Por otro lado, H. A. Gutiérrez (2016, 184) demuestra que, cuando la asignación es proporcional, esta relación se puede escribir de la siguiente manera:
\[ DEFF_p = \frac{ \sum_{h=1}^H W_h S^2_{x_{hp}} }{S^2_{x_p}} \cong 1 - R^2_p \ \ \ \ \ \ \ \ \ p = 1, \ldots, P. \]
En donde, para cada estrato \(h = 1, \ldots, H\), se tiene que \(S^2_{x_p}\) es la varianza de la variable \(x_p\) en la población y \(S^2_{x_{hp}}\) es la varianza de la variable \(x_p\) supeditada al estrato \(h\). Nótese que este efecto de diseño es función del coeficiente de determinación \(R^2_p\) en un modelo lineal con intercepto que relaciona la \(p\)-ésima variable de evaluación (respuesta) con los estratos (factores). Una ventaja de expresar el efecto de diseño como en la ecuación anterior es que no dependerá del tamaño de muestra. Una vez definido el criterio de evaluación de la estratificación sobre una variable \(x_p\), es necesario definir un criterio de estratificación multivariante que contemple cada una de las \(P\) variables. Siguiendo las ideas de Jarque (1981), se propone la siguiente medida de calidad, definida como el efecto de diseño generalizado (\(G(S)\)) sobre todas las variables de la matriz de información:
\[ G(S) = \sum_{p=1}^P DEFF_p = \sum_{p=1}^P \frac{1}{S^2_{x_p}}\sum_{h=1}^H W_h S^2_{x_{hp}} \]
Ante una estratificación pertinente, se esperaría que \(Var_{ST}(\bar x _p) < Var_{SI}(\bar x _p)\), por lo tanto \(0 < DEFF_p < 1\), lo que conlleva a que \(0 < G(S) < P\). Luego, se debería escoger el escenario para el cual \(G(S)\) fuera mínimo. Nótese que, para cada uno de los escenarios en estudio, es necesario fijar el número de estratos; en general se propende a que el número de estratos esté entre tres y cinco. Esta escogencia del número de grupos debe ser discutida al interior del INE con los equipos que determinan la rotación de las UPM en cada periodo de levantamiento de las encuestas de hogares. Escoger un número alto de estratos reducirá la varianza, pero a su vez puede tener repercusiones negativas en la logística de rotación del diseño de muestreo de las encuestas, haciendo que se agoten rápidamente las UPM dentro de los estratos geográficos y socioeconómicos. Por lo anterior, se recomienda restringir los escenarios de evaluación a la consideración de \(H=3\) y \(H=4\) estratos.
El siguiente cuadro ejemplifica la evaluación de estas técnicas para dos escenarios de estratificación (tres y cuatro estratos) en una matriz de información que contiene 8 variables. De la tabla se puede deducir varias conclusiones interesantes. Por ejemplo, para el primer indicador, la mejor estratificación es la dada por el método de raíz de frecuencia acumulada (DH) con cuatro estratos; para el segundo indicador, la mejor estratificación es la partición genética (BB) con cuatro estratos; mientras que para el último indicador, la mejor estratificación es la estratificación óptima con el algoritmo de Sethi (LH) con cuatro estratos. Como se puede notar, para cada indicador existirá un método que induzca una mayor eficiencia que para otros indicadores. Esto claramente muestra que la estratificación con respecto a un solo indicador puede ser un procedimiento inadecuado. Por lo tanto, basados en este ejemplo, el mejor método sería el de Dalenious-Hidiroglou (DH) con cuatro estratos, puesto que induce una mayor eficiencia conjunta al reducir el efecto de diseño generalizado.
| DEFF | Q (H=3) | DH (H=3) | LH (H=3) | GH (H=3) | KmJ (H=3) | BB (H=3) | Q (H=4) | DH (H=4) | LH (H=4) | GH (H=4) | KmJ (H=4) | BB (H=4) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| \(\bar x_1\) | 0.87 | 0.85 | 0.81 | 0.82 | 1 | 0.88 | 0.8 | 0.70 | 0.76 | 0.72 | 0.71 | 0.77 |
| \(\bar x_2\) | 0.89 | 0.82 | 0.95 | 0.97 | 0.94 | 0.88 | 0.79 | 0.74 | 0.75 | 0.77 | 0.75 | 0.71 |
| \(\bar x_3\) | 0.87 | 0.97 | 0.83 | 0.96 | 0.89 | 0.95 | 0.74 | 0.75 | 0.79 | 0.7 | 0.79 | 0.71 |
| \(\bar x_4\) | 0.92 | 0.89 | 0.81 | 0.94 | 0.96 | 1 | 0.77 | 0.73 | 0.73 | 0.7 | 0.71 | 0.74 |
| \(\bar x_5\) | 0.85 | 0.83 | 0.96 | 0.96 | 0.83 | 0.81 | 0.8 | 0.73 | 0.8 | 0.78 | 0.8 | 0.79 |
| \(\bar x_6\) | 0.87 | 0.88 | 0.9 | 0.88 | 0.86 | 0.81 | 0.8 | 0.72 | 0.76 | 0.7 | 0.74 | 0.73 |
| \(\bar x_7\) | 0.87 | 0.95 | 0.99 | 0.83 | 0.86 | 0.84 | 0.75 | 0.7 | 0.77 | 0.72 | 0.77 | 0.77 |
| \(\bar x_8\) | 0.93 | 0.82 | 0.91 | 0.99 | 0.93 | 0.88 | 0.77 | 0.74 | 0.72 | 0.78 | 0.76 | 0.75 |
| G(S) | 7.07 | 7.01 | 7.16 | 7.35 | 7.27 | 7.05 | 6.22 | 5.81 | 6.08 | 5.87 | 6.03 | 5.97 |
Para estudiar la comparabilidad y consistencia del proceso de estratificación, los algoritmos de evaluación se deberían aplicar sobre cada una de las UPM en las áreas urbanas, pero independientemente de las UPM rurales.Si la ganancia en eficiencia es mayor en este escenario, se pueden definir los estratos de forma independiente. Si, por el contrario, la comparabilidad entre estratos es imperante en el proceso de estratificación, se puede considerar únicamente el escenario conjunto en donde las UPM de la zona urbana y rural están presentes conjuntamente. En este último caso, la clasificación de las UPM de la zona urbana se regirá por las mimas condiciones que sus contrapartes urbanas.
Al margen de la técnica utilizada para encontrar la mejor clasificación de las UPM, se recalca que la viabilidad sobre el número de estratos sea discutida de forma exhaustiva por todas las áreas involucradas al interior de los INE. En forma general, es recomendable restringir los escenarios de evaluación a la consideración de H=3 o H=4 estratos. Este último componente es importante puesto que los diseños de muestreo deberían considerar un tamaño de muestra mínimo de dos UPM por estrato para poder estimar la varianza del estimador (H. A. Gutiérrez 2016).
El efecto diseño no es el único aspecto por evaluar para la elección del procedimiento de estratificación. Es necesario verificar la estabilidad del método con respecto a los otros procedimientos de estratificación. Por ejemplo, la siguiente tabla muestra la matriz de coincidencias entre las diferentes clasificaciones de los estratos.
| Técnica | Jarque | K-means | DAL | GEO | LH-S | LH-K | Percentil |
|---|---|---|---|---|---|---|---|
| Q | 1 | 0,64 | 0,92 | 0,84 | 0,89 | 0,89 | 0,82 |
| DH | 0,64 | 1 | 0,68 | 0,62 | 0,71 | 0,71 | 0,74 |
| LH | 0,92 | 0,68 | 1 | 0,82 | 0,96 | 0,96 | 0,90 |
| GH | 0,84 | 0,62 | 0,82 | 1 | 0,78 | 0,78 | 0,73 |
| KmJ | 0,89 | 0,71 | 0,96 | 0,78 | 1 | 1,00 | 0,93 |
| BB | 0,89 | 0,71 | 0,96 | 0,78 | 1,00 | 1 | 0,93 |
Por último, también se debe evaluar la coherencia de la distribución de las diferentes variables agregadas a nivel de UPM en los estratos. Por ejemplo, la proporción de personas mayores de 15 años alfabetizadas debería tener mayor incidencia en los estratos más altos, y este patrón también se debería observar para diferentes indicadores como la proporción de hogares con internet, la proporción de tenencia de refrigerador, la proporción de tenencia de televisión por cable, la proporción de tenencia de automóvil, la proporción de hogares con saneamiento adecuado, la proporción de hogares con pisos adecuados, la proporción de personas con educación superior, entre otras. La figura 5.2 muestra el comportamiento esperado en los estratos de muestreo para algunas variables de interés. De esta forma, el estrato uno debería presentar condiciones económicas más adversas, el estrato dos debería tener mejores condiciones, siendo el tercer estrato el que agrupa a las UPM con menores dificultades socioeconómicas. En el área rural debiesen aparecer una menor proporción de UPM en el estrato 3, dadas las condiciones menos favorables.
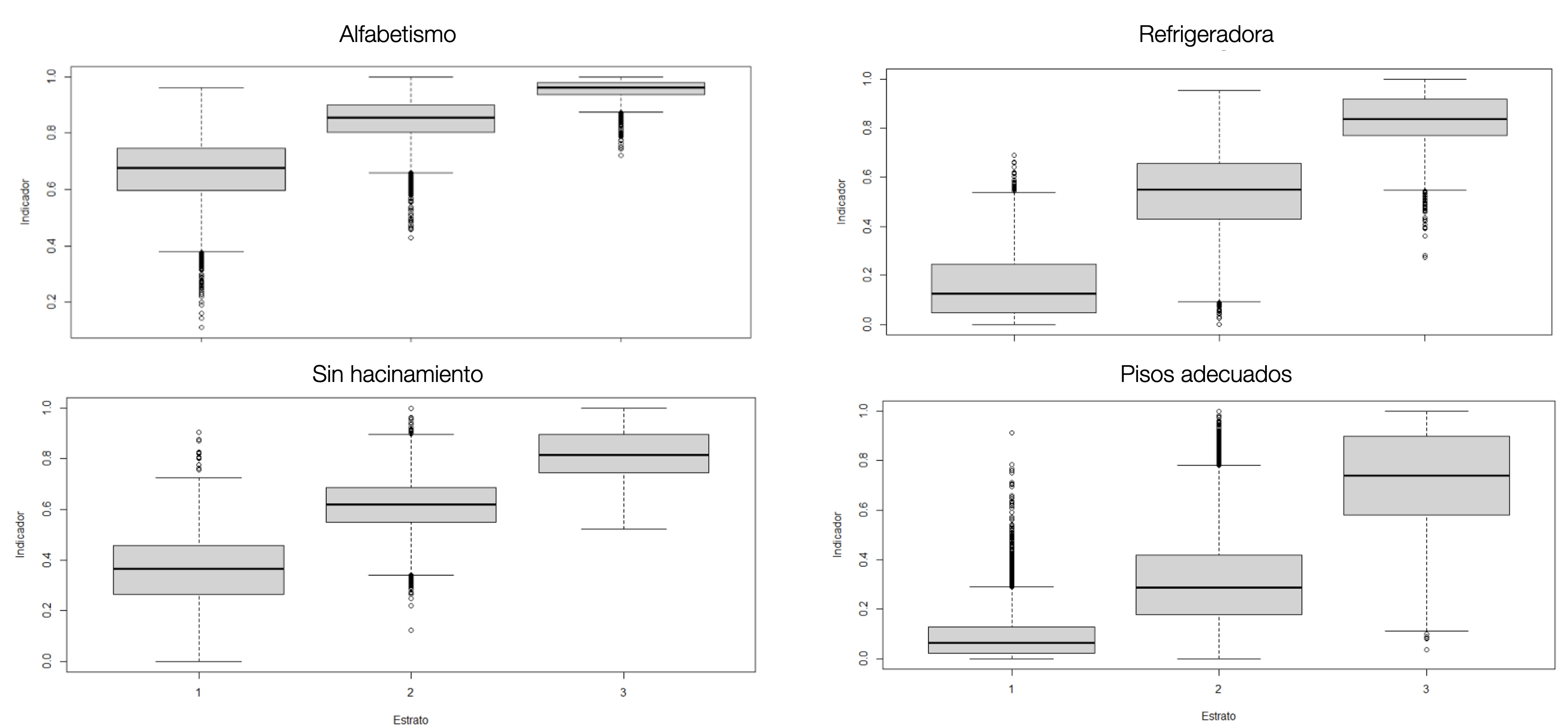
Figura 5.2: Comportamiento esperado en los estratos de muestreo para algunas variables de interés.
Si la contribución de algunas unidades al total poblacional es no significativa, y además esas unidades son de difícil acceso, es común que en algunos países de la región se opte por redefinir el universo y crear un estrato de exclusión forzosa. En este estrato no se realiza ninguna encuesta y las respectivas estimaciones no tendrán en cuenta a esta población excluida. Por último, como algunos procedimientos de clasificación se basan en la generación de números aleatorios, se recomienda documentar los códigos computacionales que se utilizaron para que los resultados puedan ser replicados, por lo que debe fijar una semilla aleatoria al comienzo del código computacional.