13.2 Soluciones
Como se expuso en la sección anterior, si no hay correlación entre la variable de interés y la estructura de la ausencia de respuesta entonces no hay sesgo en los estimadores. Esto quiere decir que, si la probabilidad de respuesta es homogénea (representatividad fuerte) o pudiera modelarse (representatividad débil) para todos los individuos, entonces el sesgo se podría eliminar. En esta sección se explorarán dos caminos que, al incorporar información auxiliar, eliminan el sesgo causado por el fenómeno de la ausencia de respuesta.
Ambas opciones, ajuste de factores de expansión mediante modelos de propensity score y estimadores de calibración, descansan en el paradigma de la inferencia basada en el diseño de muestreo y por ende se contemplan como dos posibilidades atractivas que mantienen la buenas propiedades de la estimación directa en encuestas de hogares.
13.2.1 Propensity Score
Como se mencionó anteriormente, uno de los ajustes que se debe realizar en la generación de los ponderadores finales es la corrección por ausencia de respuesta. En donde
\[d_{4k} = \frac{d_{3k}}{\hat{\phi_k}}\]
Como ya se había mencionado en los capítulos anteriores, si el patrón de ausencia de respuesta es NMAR, entonces \(\phi_k = f(\mathbf{y}_k, \beta)\) y en este caso, como no es posible tener acceso a los determinantes de la respuesta (porque precisamente son las mismas variables de interés en la encuesta), entonces no es posible estimar el patrón de ausencia de respuesta. Por ende, en este escenario habrá sesgo siempre. Por el contrario, si el patrón de ausencia de respuesta es MCAR o MAR, entonces \(\phi_k = f(\mathbf{x}_k, \boldsymbol{\beta})\); en este caso, si fuese posible tener acceso a las covariables \(\mathbf{x}\) que determinan el mecanismo de respuesta, entonces es posible estimar las probabilidades de respuesta mediante \(\hat{\phi}_k = f(\mathbf{x}_k, \hat{\boldsymbol{\beta}})\). Efectivamente, en el caso del estimador de Horvitz-Thompson, el sesgo del estimador se anula puesto que
\[\begin{align*} E(\hat{t}_y) &= E\left(\sum_{k\in s_r}d_{3k}y_k\right) \\ &= E\left(\sum_{k\in s_r}\frac{y_k}{\pi_k \hat{\phi_k}}\right)\\ &= E\left(E\left(\sum_{k\in U}\frac{y_k}{\pi_k \hat{\phi_k}}I_kD_k|I_k\right)\right)\\ &= \sum_{k\in U}\frac{y_k}{\pi_k \hat{\phi_k}}E\left(I_k\right)E\left(D_k|I_k\right)\\ &= \sum_{k\in U}\frac{y_k}{\pi_k \hat{\phi_k}}\pi_k\phi_k = t_y \end{align*}\]
Asumiendo que el modelo está bien establecido, entonces se tendrá una concordancia directa entre \(\hat{\phi_k}\) y \(\phi_k\); por lo tanto se anularían en la última igualdad de la ecuación anterior. Además, el insesgamiento viene supeditado puesto que,
\[ E(I_kD_k) = E\left(E(I_kD_k|I_k) \right) = E(I_k)E(D_k|I_k) = \pi_k \phi_k \]
En resumen, si se tiene acceso a información auxiliar (contenida en el marco de muestreo o en otras preguntas de la encuesta), y si se considera que el mecanismo que genera la ausencia de respuesta en la encuesta de hogares es MAR o MCAR, es posible ajustar un modelo de propensity score para la ausencia de respuesta (en donde la variable dependiente es una variable indicadora de la respuesta del individuo por lo general supeditado a una distribución Bernoulli o Binomial). En resumen, es posible definir el siguiente estimador insesgado
\[ \hat{t}_y=\sum_{k\in s_{ER}}d_{4k}y_k \]
En donde
\[ d_{4k} = \frac{d_{3k}}{\hat{\phi_k}} \ \ \ \ \ \ \ \ \forall \ k \in s_{ER} \]
Siempre es muy importante realizar una validación exhaustiva de los modelos utilizados para estimar la probabilidad de respuesta. En general, es necesario que el modelo satisfaga las siguientes dos condiciones:
- Soporte común: al igual que en un experimento aleatorizado, es necesario garantizar que ninguna combinación de las covariables induzca un estado (respuesta o ausencia de respuesta) de forma determinística. Es decir sobre todas las combinaciones en las covariables deben existir respondientes y no respondientes. Esta condición se puede escribir como: \[ 0 < Pr(D_{1,k} = 1 |\mathbf{x}_{1}) < 1 \]
- Balanceo: como la respuesta de las unidades de muestreo no provienen de un estudio aleatorizado, es necesario garantizar que la distribución de las \(\hat\phi_k\) sea similar entre respondientes y no respondientes. De esta forma, es posible expandir el subconjunto de respondientes efectivos a la muestra original (que incluye a las unidades no respondientes), la cual a su vez expande a toda la población de interés. Esta condición se puede escribir como:
\[\begin{align*} \hat\phi_{1, k} &= Pr[D_{1, k} | I_{1, k} = 1,\mathbf{x}] \\ &= Pr[D_{1, k} | k \in s_r, I_{1, k} = 1, \mathbf{x}] \\ &= Pr[D_{1, k} | k \notin s_r, I_{1, k} = 1, \mathbf{x}] \end{align*}\]
Por último, se debe corroborar que la suma de los pesos ajustados por la ausencia de respuesta esté cercana al tamaño de la población que se quiere representar. La figura 13.1 permite ilustrar el soporte común entre respondientes y no respondientes para un modelo de propensity score; nótese que ambas distribuciones son similares, por lo que es posible concluir que efectivamente las covariables usadas están representando bien la estructura estocástica en respondientes y no respondientes.
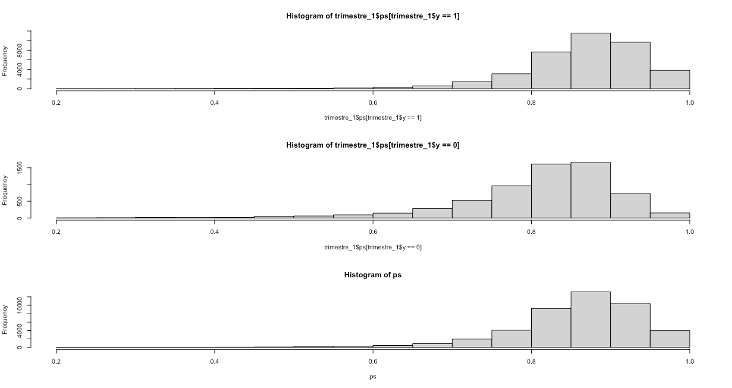
Figura 13.1: Distribución de las probabilidades estimadas de respuesta: respondientes (arriba), no respondientes (medio), ambos (abajo).
Además, la figura 13.2 muestra la propiedad de balanceo en el modelo; véase cómo ambas distribuciones se alejan de los extremos (ceros y uno) y presentan una caracterización similar.
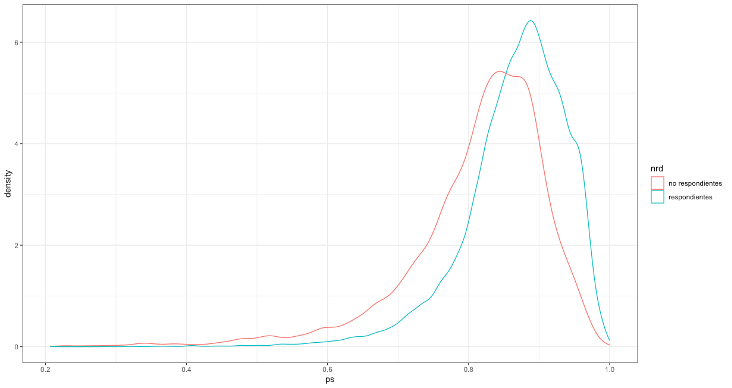
Figura 13.2: Balanceo entre respondientes y no respondientes
13.2.2 Calibración
Como lo afirma C.-E. Särndal (2007), la calibración provee una forma sistemática para involucrar la información auxiliar. En la mayoría de aplicaciones prácticas, la calibración provee un enfoque simple para incorporar esta información dentro de la etapa de estimación. La información auxiliar fue usada para mejorar la precisión de los estimativos mucho antes que el término calibración fuera popular. La calibración puede ser usada efectivamente en encuestas donde la información auxiliar está disponible en diferentes niveles. Por ejemplo, al realizar un muestreo en dos etapas la información auxiliar puede existir para las unidades de la primera etapa (los conglomerados) y puede existir otra información para las unidades de la segunda etapa (elementos o conglomerados).
Como se ha detallado con amplitud en este y los capítulos anteriores, la ausencia de respuesta de unidad tiene consecuencias dañinas en la inferencia con encuestas de hogares. En este caso es altamente recomendable que se implemente ajuste a los factores de ponderación de las unidades (hogares o personas). A pesar de que los modelos de propensity score tienen una larga trayectoria en el manejo de la ausencia de respuesta, la calibración utilizada para corregir estos sesgos ofrece una relativamente nueva perspectiva. Nótese que el estimador tradicional toma la siguiente forma:
\[ \hat t_y^* = \sum_{s_r} w_k\ y_k = \sum_{s_r} \frac{d_k}{\phi_k} y_k \]
Esta anterior expresión indica que implícitamente se genera un procedimiento en dos etapas en donde, en primer lugar, se calculan lo pesos básicos inducidos por el diseño de muestreo, luego se ajusta un modelo de propensity score para estimar las probabilidades de respuesta \(\phi_k\). A esta estrategia generalmente se le agrega una tercera etapa en donde se crean nuevos pesos calibrados con respecto a proyecciones demográficas post-censales, como por ejemplo los cruces entre edad, sexo y región. Al ajustar los pesos para que sumen exactamente la cifra de las proyecciones censales, se reduce el sesgo de subcobertura.
C.-E. Särndal (2007) afirma que la práctica general es asumir que el estimador \(\hat t_y^*\) es insesgado, cuando en realidad no lo es, puesto que no es posible conocer todos los determinantes del mecanismo de respuesta para ajustar el modelo que estima las probabilidades de respuesta. Además, de la sección anterior se deduce que este supuesto implica que se considere que \(\pi_k \hat\phi_k\) es la verdadera probabilidad de inclusión de la unidad, cuando en realidad no es así. Por lo tanto, realizar un ajuste a los factores de expansión únicamente basados en los modelos de propensity score traerá inevitablemente una cierta cantidad de sesgo en la estimación de los parámetros en las encuestas de hogares.
Bajo este escenario, el enfoque de calibración doble surge como un proceso metodológico adicional que pretende corregir estos sesgos. Para poder utilizarlo, es necesario tener información auxiliar en dos niveles: la población y la muestra. Este tipo de metodologías pueden ser usadas en las encuestas tipo panel, o panel rotativo. En este proceso es necesario contar con dos tipos de información auxiliar:
- Por un lado tendremos la información poblacional usual que se utiliza para calibrar los factores de expansión en un levantamiento regular. Las variables que intervienen en esta calibración las notaremos como \(\boldsymbol{x}_{1k}\) y por lo general denotan la pertenencia de los individuos a regiones, o grupos de edad, sexo o área (urbano, rural).
- Por otro lado deberemos tener acceso a información auxiliar en la muestra original (que incluya a las unidades respondientes y no respondientes) y que notaremos como \(\boldsymbol{x}_{2k}\). Por ejemplo, utilizando la información del panel al momento de la primera medición, sería posible contar con información concerniente a la condición de ocupación, ingresos, o cualquier otra variable medida en la primera oleada del panel.
Por lo tanto, es posible calibrar los pesos en la muestra de respondientes (\(s_r\)) a nivel de la información auxiliar disponible en la muestra original (\(s\)), y luego a nivel nacional (\(U\)) o por los estratos de interés. Si el mecanismo que genera la ausencia de respuesta es MAR o MCAR, es posible que los ponderadores de calibración eliminen el sesgo en las estimaciones finales si es que las variables que generan este mecanismo se han calibrado en alguno de las dos niveles mencionados. C.-E. Särndal y Lundström (2006) proponen que, para lograr este objetivo, se encuentre un primer conjunto de pesos calibrados sujetos a la siguiente restricción:
\[ \sum_{s}w_{1k}\boldsymbol{x}_{1k} = \sum_{U}\boldsymbol{x}_{1k} \]
Luego, en una segunda etapa, se deben usar estos pesos intermedios \(w_{1k}\) para calcular los pesos finales de calibración \(w_{k}\) de la muestra de respondientes efectivos que están sujetos a la siguiente restricción:
\[ \sum_{s_r}w_{k}\boldsymbol{x}_{2k} = \sum_{s}w_{1k}\boldsymbol{x}_{k} = \begin{pmatrix} \sum_{U}\boldsymbol{x}_{1k}\\ \sum_{s_r}w_{1k}\boldsymbol{x}_{2k} \end{pmatrix} \]
En este sentido, nótese que la forma funcional de los pesos de calibración doble resultantes de este proceso de optimización se pueden escribir de la siguiente manera:
\[ w_k = d_k \times g_k \cong d_k \times \hat \phi_k \]
Por ende, bajo el raciocinio de la calibración, los pesos \(g_k\) se pueden ver como una estimación de las probabilidades de respuesta \(\phi_k\). Por otra parte, de las expresiones, sobre el sesgo de los estimadores que no contienen ningún tipo de corrección, se puede notar que el sesgo se propaga a través de las variables de la encuesta y se propaga con más fuerza en las variables correlacionadas con los determinantes de la ausencia de respuesta.
Para mostrar cómo el ajuste a los factores de expansión, con las dos metodologías anteriormente mencionadas, inducen menor sesgo que los estimadores comunes, se planeó el siguiente experimento:
- Se generó una población compuesta por individuos con diferente propensión de respuesta MCAR.
- Se utilizaron metodologías de calibración y se comparó, de forma empírica, el efecto de la ausencia de respuesta sobre las estimaciones finales.
En primera instancia, cabe mencionar que la población se definió a partir del ingreso del hogar, y se creó usando variables auxiliares disponibles (sexo). De esta forma, se le dio una probabilidad de respuesta diferencial entre los grupos correspondientes al cruce de las categorías de estas dos variables. Como resultado de las simulaciones, se generaron estimaciones para el estimador de Horvitz-Thompson sin ajuste de ningún tipo y para un estimador de calibración que tuvo en cuenta los conteos poblacionales censales para cada las dos categorías de la variables sexo. La figura 13.3 muestra el comportamiento de ambas estimaciones. La línea roja refleja el parámetro desconocido, los puntos negros indican las estimaciones del estimador de calibración en cada iteración de la simulación, mientras que los puntos grises muestran las estimaciones del estimador de Horvitz-Thompson en cada iteración de la simulación
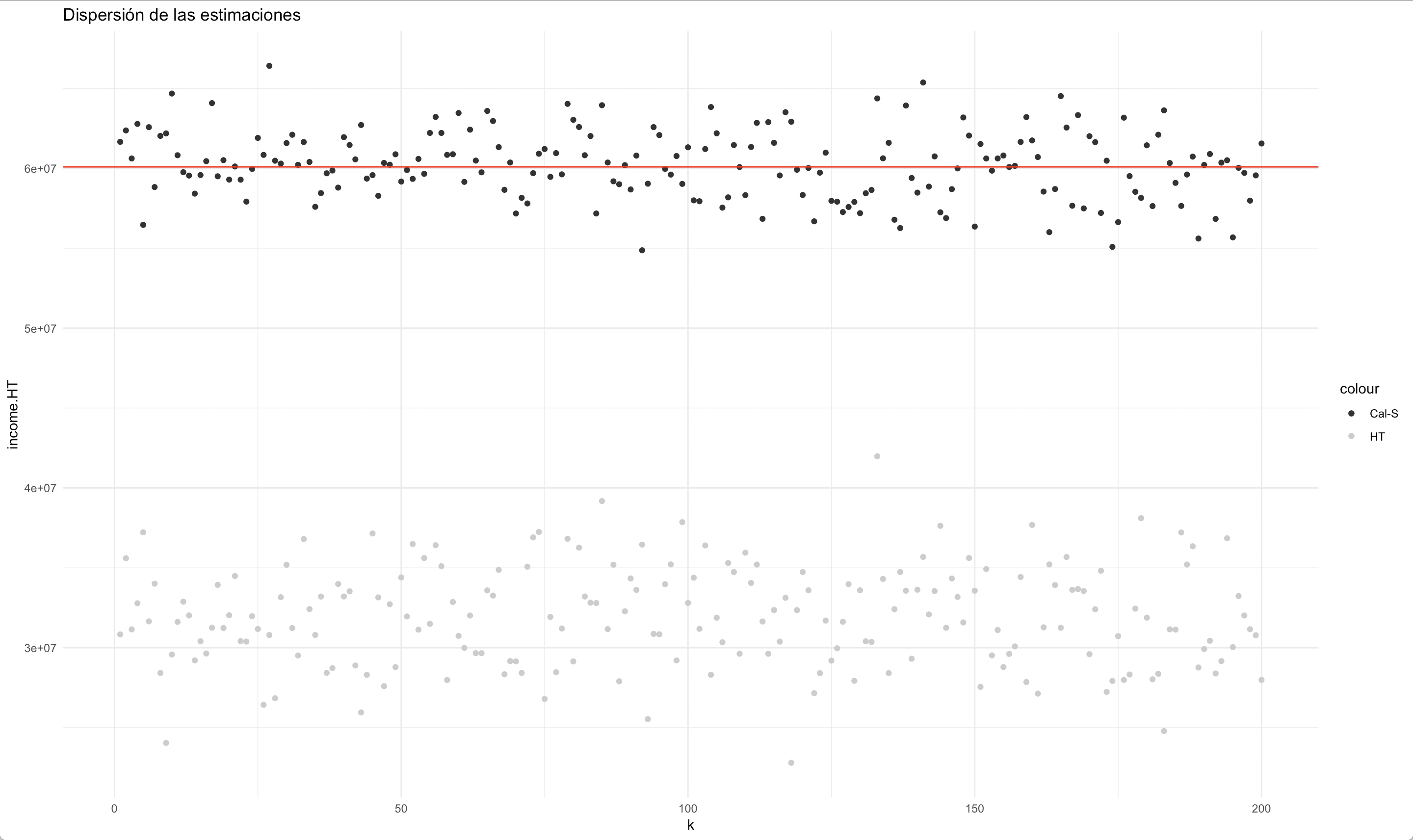
Figura 13.3: Estimaciones de Horvtiz-Thompson y de calibración.
En conjunto con la gráfica anterior, la figura 13.4 muestra la distribución sesgada del estimador de Horvitz-Thompson (gris) en comparación con el insesgamiento del estimador de calibración (negro). Bajo este esquema de respuesta, incluir en la calibración las variables pertinentes corrige el sesgo generado por la ausencia de respuesta. En este estudió se encontró que el estimador ingenuo (HT) produjo sesgo para la estimación de los tamaños de hombres y mujeres, para el tamaño de la población, para los ingresos de hombres y mujeres y para los ingresos de la población.
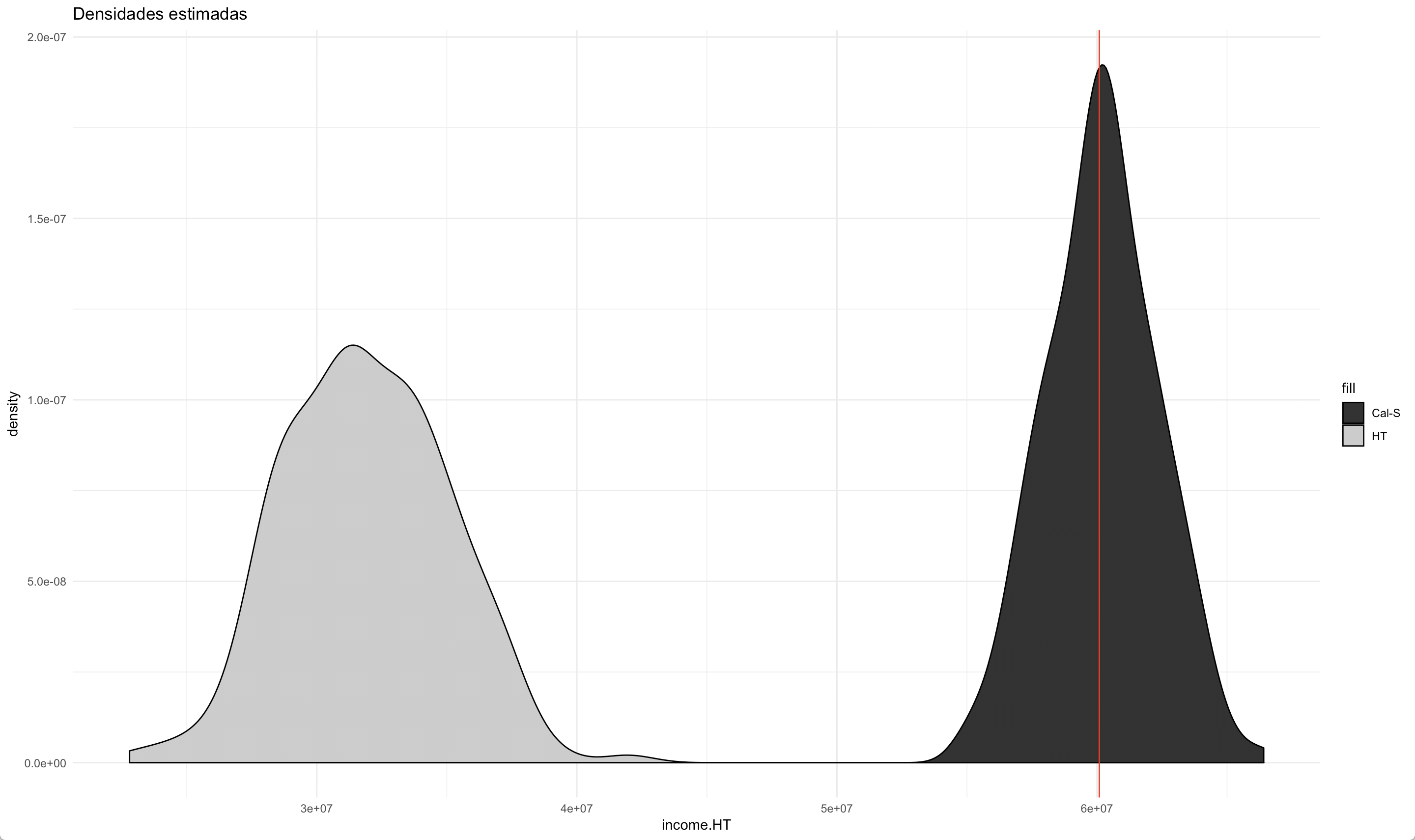
Figura 13.4: Distribuciones del estimador de Horvtiz-Thompson y del estimador de calibración
Como se mencionó anteriormente, hay mejores formas de calibrar, puesto que el problema de la calibración se reduce a cómo introducir la información auxiliar en la estructura de estimación de la encuesta, es posible que existan variables que reduzcan el sesgo, pero no todas las variables inducirán el mismo nivel de precisión. Al momento de escoger, se deberían seleccionar aquellas variables que reduzcan el sesgo y que además reduzcan la varianza. Por tanto, las variables auxiliares que se usen como insumo en los procesos de calibración deben:
- Ser capaces de explicar la variación de la probabilidad de respuesta.
- Estar correlacionadas con las variables de interés.
- Identificar los dominios de estimación más importantes.
En particular al introducir otras covariables en la calibración (grupo de edad, escolaridad, región, área), además de la corrección del sesgo se evidencia un aumento de la precisión en las nuevas estimaciones, tal como lo muestra las distribuciones de los estimadores en la figura 13.5, en donde se consideran tres estimadores: el estimador de Horvitz-Thompson (gris claro), el estimador de calibración con restricción de sexo (negro) y el estimador de calibración con todas las restricciones (gris oscuro).
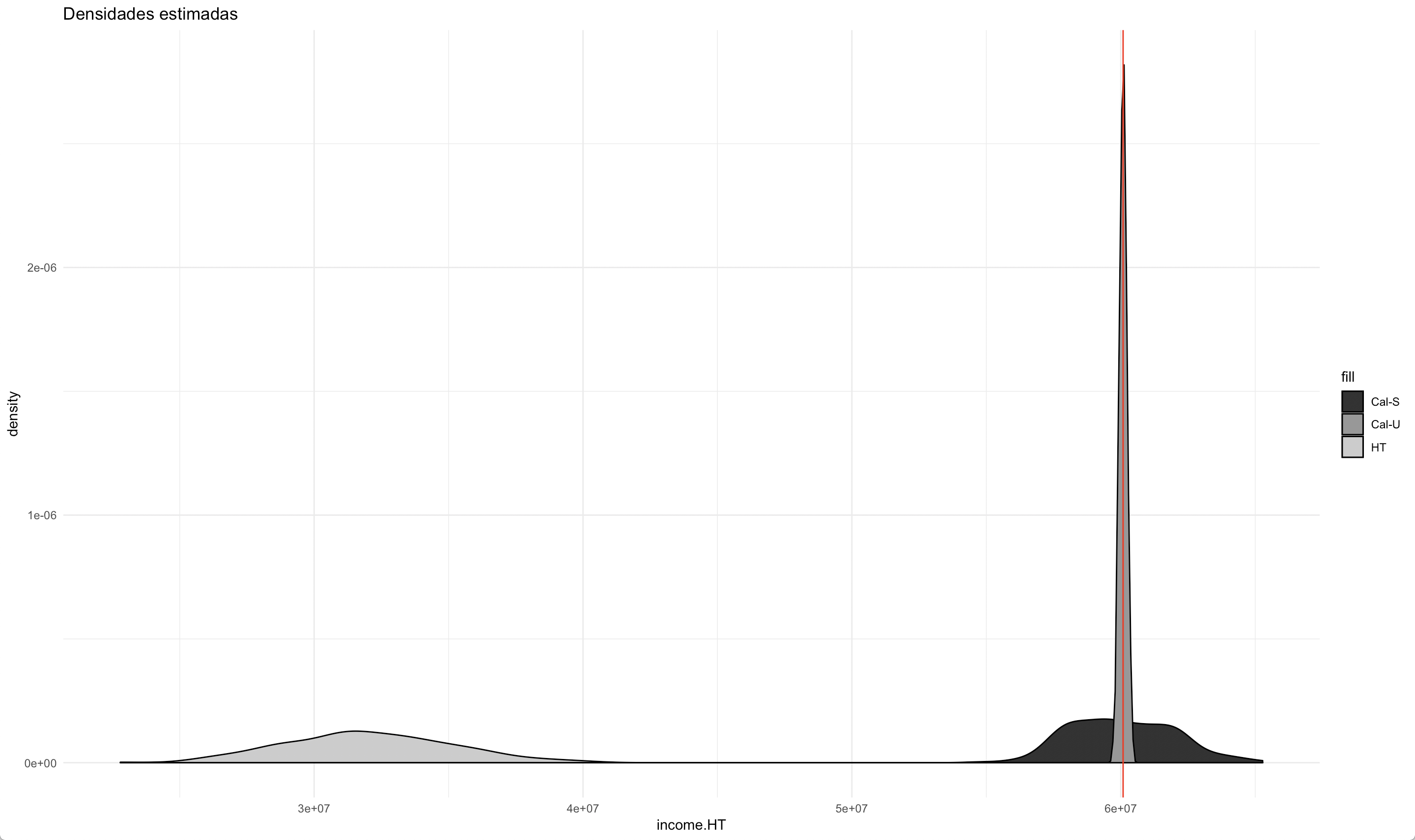
Figura 13.5: Distribuciones del estimador de Horvtiz-Thompson y de dos estimadores de calibración